题目内容
7.画出求$\frac{1}{1+{2}^{2}}$+$\frac{1}{2+{3}^{2}}$+$\frac{1}{3+{4}^{2}}$+…+$\frac{1}{99+10{0}^{2}}$的值的算法框图,并编写基本算法语句.分析 由已知中,程序的功能我们可以利用循环结构来解答本题,由于这是一个累加问题,故循环前累加器S=0,由于已知中的式子,可得循环变量k初值为1,步长为1,终值为99,累加量为$\frac{1}{k+(k+1)^{2}}$,由此易写出算法步骤,并画出程序框并编写基本算法语句.
解答 解:程序框图如下:
算法语句如下:
S=0,k=1
FOR k=1 TO 99
S=S+1/(k^2+3*k+1)
NEXT
PRINT S
END
点评 本题考查的知识点是程序框图解决实际问题,其中利用循环解答累加问题时,关键是根据已知中的程序确定循环变量的初值、步长、终值,及累加量的通项公式,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
1.在△ABC中,内角A,B,C所对的边长分别为a,b,c.asinBcosC+csinBcosA=$\frac{1}{2}$b且a>b,则∠B=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
12.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+4,x<0\\ x{e^x},x≥0\end{array}$,若f(x1)=f(x2)(x1<x2),则$\frac{{f({x_2})}}{x_1}$的取值范围为( )
| A. | (-∞,0] | B. | [1,+∞) | C. | (-∞,0) | D. | (-∞,0)∪(0,+∞) |
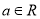 ,则“
,则“ ”是“
”是“ ”的( )
”的( ) 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )