题目内容
5.已知命题p:x2-8x-20≤0,q:1-m≤x≤1+m(m>0),若p是q的充分不必要条件,求实数m的取值范围.分析 由p:x2-8x-20≤0,由于p是q的充分不必要条件,可得[-2,10]?[1-m,1+m].解出即可得出.
解答 解:由p:x2-8x-20≤0,得-2≤x≤10,
∵p是q的充分不必要条件,
∴[-2,10]?[1-m,1+m].
则$\left\{\begin{array}{l}1-m<-2\\ 1+m≥10\end{array}\right.$,或$\left\{\begin{array}{l}1-m≤-2\\ 1+m>10\end{array}\right.$,
解得m≥9.
故实数m的取值范围为[9,+∞).
点评 本题考查了不等式的解法及其性质、充要条件的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
15.已知集合A={-1,0,1,2},B={x|log2(x+1)>0},则A∩B=( )
| A. | {-1,0} | B. | {1,2} | C. | {0,2} | D. | {-1,1,2} |
16.已知直线l的方程为x+my-2=0,则直线l( )
| A. | 恒过点(-2,0)且不垂直x轴 | B. | 恒过点(-2,0)且不垂直y轴 | ||
| C. | 恒过点(2,0)且不垂直x轴 | D. | 恒过点(2,0)且不垂直y轴 |
20.执行如图所示的程序框图,若输入x为13,则输出y的值为( )


| A. | 10 | B. | 5 | C. | 4 | D. | 2 |
14. 设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点为F1、F2,左右顶点为A1,A2,双曲线C2的焦点为A1,A2,顶点为F1,F2,椭圆C1与双曲线C2交于P1,P2,P3,P4四点,若直线P2P4的斜率为$\frac{1}{2}$,则椭圆C1的离心率为( )
设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点为F1、F2,左右顶点为A1,A2,双曲线C2的焦点为A1,A2,顶点为F1,F2,椭圆C1与双曲线C2交于P1,P2,P3,P4四点,若直线P2P4的斜率为$\frac{1}{2}$,则椭圆C1的离心率为( )
 设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点为F1、F2,左右顶点为A1,A2,双曲线C2的焦点为A1,A2,顶点为F1,F2,椭圆C1与双曲线C2交于P1,P2,P3,P4四点,若直线P2P4的斜率为$\frac{1}{2}$,则椭圆C1的离心率为( )
设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点为F1、F2,左右顶点为A1,A2,双曲线C2的焦点为A1,A2,顶点为F1,F2,椭圆C1与双曲线C2交于P1,P2,P3,P4四点,若直线P2P4的斜率为$\frac{1}{2}$,则椭圆C1的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
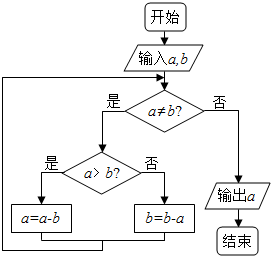 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为6,4,则输出a的值为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为6,4,则输出a的值为( ) 如图,在边长为3的正方形内有一半径为1的圆,随机地向正方形内丢一粒豆子,则它落在圆内的概率为$\frac{π}{9}$.
如图,在边长为3的正方形内有一半径为1的圆,随机地向正方形内丢一粒豆子,则它落在圆内的概率为$\frac{π}{9}$.