题目内容
9.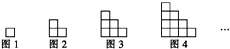 如图所示图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第17个图形中小正方形的个数是153.
如图所示图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第17个图形中小正方形的个数是153.
分析 由a2-a1=2,a3-a2=3,a4-a3=4,可推测an-an-1=n,以上式子累加,结合等差数列的求和公式可得答案.
解答 解:a1=1,a2=3,a3=6,a4=10,所以a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n,等式两边同时累加得an-a1=2+3+…+n,即an=1+2+…+n=$\frac{n(n+1)}{2}$,所以第17个图形中小正方形的个数是153.
故答案为:153.
点评 本题考查归纳推理,由数列的前几项得出an-an-1=n是解决问题的关键,属基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
19.“x2+5x-6>0”是“x>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.若圆x2+y2-2x-4y+1=0关于直线ax-by=0(a>0,b>0)对称,则双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1的渐近线方程为( )
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
1.已知等比数列a1,a2,a3,a4满足a1∈(0,1),a2∈(1,2),a3∈(2,4),则a4的取值范围是( )
| A. | (3,8) | B. | (2,16) | C. | (4,8) | D. | $(2\sqrt{2},16)$ |
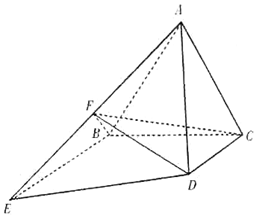 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.