题目内容
20.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,右焦点为F2,点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点.若△PF2Q的周长为4,则椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.分析 设P(x1,y1),Q(x2,y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2-|OM|2求出|PQ|,利用△PF2Q的周长为4,可得结论.
解答 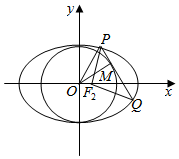 解:椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,则a=2c,b=$\sqrt{3}$c,
解:椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,则a=2c,b=$\sqrt{3}$c,
设P(x1,y1),Q(x2,y2),
∴|PF2|2=(x1-c)2+y12=$\frac{1}{4}$(x1-4c)2,
∴|PF2|=2c-$\frac{1}{2}$x1,
连接OM,OP,由相切条件知:
|PM|2=|OP|2-|OM|2=x12+y12-3c2=$\frac{1}{4}$x12,
∴|PM|=$\frac{1}{2}$x1,
∴|PF2|+|PM|=2c,
同理可求|QF2|+|QM|=2c,
∴|F2P|+|F2Q|+|PQ|=4c.
∵△PF2Q的周长为4,∴c=1,
∴$a=2,b=\sqrt{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
故答案为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
点评 本题考查的知识点是椭圆的标准方程和性质,直线与圆的位置关系,直线与椭圆的位置关系,熟练掌握椭圆的性质是解答本题的关键.

练习册系列答案
相关题目
12.今有苹果m个(m∈N+),分给10个同学,每个同学都分到苹果,恰好全部分完.第一个人分得全部苹果的一半还多一个,第二个人分得第一个人余下苹果的一半还多一个,以此类推,后一个人分得前一个人余下的苹果的一半还多一个,则苹果个数m为( )
| A. | 2046 | B. | 1024 | C. | 2017 | D. | 2018 |
9.已知集合M={x|x2≤9},N={x|x≤1},则M∩N=( )
| A. | [-3,1] | B. | [1,3] | C. | [-3,3] | D. | (-∞,1] |
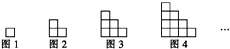 如图所示图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第17个图形中小正方形的个数是153.
如图所示图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第17个图形中小正方形的个数是153.