题目内容
若非零向量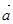 ,
, 满足
满足 ,且
,且 ,则向量
,则向量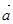 ,
, 的夹角为 ( )
的夹角为 ( )
A.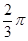 | B. | C. | D. |
A
解析试题分析:因为,非零向量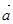 ,
, 满足
满足 ,且
,且 ,所以,
,所以, =
=  ,
, =
= ,所以,向量
,所以,向量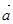 ,
, 的夹角为
的夹角为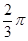 ,选A。
,选A。
考点:平面向量的数量积,平面向量的夹角。
点评:简单题,利用 求夹角。
求夹角。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
已知点 .
. .
. .
.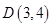 ,则向量
,则向量 在
在 方向上的投影为( )
方向上的投影为( )
A. | B. | C. | D. |
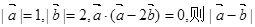 = ( )
= ( )
| A.2 | B.4 | C.1 | D.8 |
非零向量 ,
,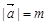 ,
, ,若向量
,若向量 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D.以上均不对 |
已知平面上 三点共线,且
三点共线,且 ,则对于函数
,则对于函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A.周期是 | B.最大值是2 |
C. 是函数的一个对称点 是函数的一个对称点 | D.函数在区间 上单调递增 上单调递增 |
在R t △PAB中,PA=PB,点C、D分别在PA、PB上,且CD∥AB,AB=3,AC= ,则
,则 的值为( )
的值为( )
| A.-7 | B.0 | C.-3 | D.3 |
在 中,
中,  ,
, 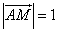 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 ,
,  , 且
, 且 , 则
, 则 等于 ( )
等于 ( ) ,
, ,对任意
,对任意 ,恒有
,恒有 ,则( )
,则( ) B.
B. C.
C. D.
D. 