题目内容
平面向量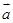 与
与 的夹角为
的夹角为 ,
,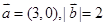 ,则
,则 = ( )
= ( )
| A.7 | B. | C. | D.3 |
C
解析试题分析:因为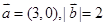 ,所以
,所以 ,
, =
=
 ,故选B.
,故选B.
考点:本题主要考查平面向量的数量积,向量模的计算。
点评:简单题,涉及平面向量模的计算,往往要“化模为方”,转化成数量积计算。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 是边长为
是边长为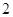 的正三角形,则
的正三角形,则 =( )
=( )
A. | B. | C.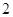 | D. |
在 中,
中,  ,
, 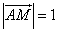 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知平面上不共线的四点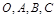 ,若
,若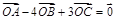 ,则
,则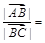
| A.3 | B.4 | C.5 | D.6 |
已知 、
、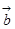 是非零向量且满足
是非零向量且满足 ,
, ,则向量
,则向量 与
与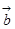 的
的
夹角是 ( )
A. | B. | C. | D. |
在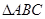 中,
中,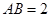 ,
,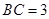 ,
,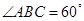 ,
,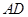 为
为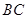 边上的高,
边上的高, 为
为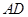 的中点,若
的中点,若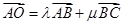 ,则
,则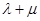 的值为()
的值为()
A.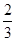 | B.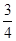 | C.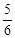 | D.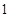 |
已知向量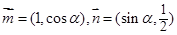 ,且
,且 ,则
,则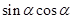 等于
等于
A. | B.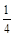 | C. | D. |
对于直角坐标平面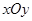 内的点
内的点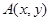 (不是原点),
(不是原点),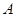 的“对偶点”
的“对偶点”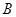 是指:满足
是指:满足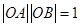 且在射线
且在射线 上的那个点. 若
上的那个点. 若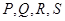 是在同一直线上的四个不同的点(都不是原点),则它们的“对偶点”
是在同一直线上的四个不同的点(都不是原点),则它们的“对偶点”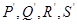 ( )
( )
| A.一定共线 | B.一定共圆 |
| C.要么共线,要么共圆 | D.既不共线,也不共圆 |
 ,
, ,对任意
,对任意 ,恒有
,恒有 ,则( )
,则( ) B.
B. C.
C. D.
D. 