题目内容
16.若非零向量$\overrightarrow a$,$\overrightarrow b$满足|$\overrightarrow a$|=|$\overrightarrow a$+$\overrightarrow b$|=2,|$\overrightarrow b$|=1,则向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为-$\frac{1}{4}$.分析 运用向量的平方即为模的平方,计算可得$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$,再由向量夹角公式:cos<$\overrightarrow a$,$\overrightarrow b$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$,计算即可得到所求值.
解答 解:由非零向量$\overrightarrow a$,$\overrightarrow b$满足|$\overrightarrow a$|=|$\overrightarrow a$+$\overrightarrow b$|=2,|$\overrightarrow b$|=1,
可得|$\overrightarrow{a}$|2=|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}$•$\overrightarrow{b}$=4,
则$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$,
即有向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{2×1}$=-$\frac{1}{4}$.
故答案为:-$\frac{1}{4}$.
点评 本题考查向量数量积的夹角公式的运用,考查向量数量积的性质:向量的平方即为模的平方,考查运算能力,属于中档题.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
 某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )| A. | 14,9.5 | B. | 9,9 | C. | 9,10 | D. | 14,9 |
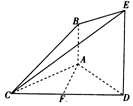 如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.
如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.