题目内容
21.(本题满分12分)
已知实数 为常数,函数
为常数,函数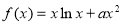 .
.
(Ⅰ)若曲线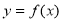 在
在 处的切线过点A
处的切线过点A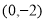 ,求实数
,求实数 值;
值;
(Ⅱ)若函数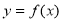 有两个极值点
有两个极值点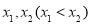 .
.
求证: ,②求证:
,②求证: .
.
(1)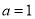 ,(2)证明见解析;
,(2)证明见解析;
【解析】
试题分析:已知曲线在某点的切线过点A,应先求切线方程,利用导数的几何意义,求出斜率,利用点斜式写直线方程,又过点A,满足直线方程,求出A;第二步①函数有两个极值点说明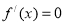 有两个不等实根,问题转化为研究函数
有两个不等实根,问题转化为研究函数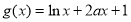 的图象与x轴何时有两个交点问题,对函数
的图象与x轴何时有两个交点问题,对函数 求导,在
求导,在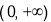 上研究函数的单调性与极值,经过对A的分类讨论发现,当A<0时,先减后增有极大值,当极大值大于零时,
上研究函数的单调性与极值,经过对A的分类讨论发现,当A<0时,先减后增有极大值,当极大值大于零时, 的图象与x轴有两个交点,解出A的范围,问题获得证明;②借助①的结论当
的图象与x轴有两个交点,解出A的范围,问题获得证明;②借助①的结论当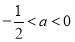 时,
时,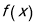 有两个极值点
有两个极值点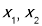 ,通过列表观察
,通过列表观察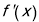 的符号与函数
的符号与函数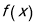 的单调性,由于
的单调性,由于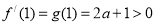 ,而
,而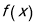 在
在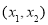 上为增函数,说明
上为增函数,说明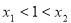 ,即
,即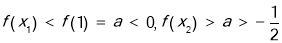 ,问题得证;
,问题得证;
试题解析:(Ⅰ)【解析】
由已知: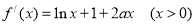 ,切点
,切点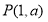 ,
,
切线方程: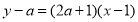 ,把
,把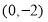 代入得:
代入得: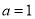
(Ⅱ)①证明:依题意: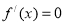 有两个不等实根
有两个不等实根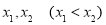 ,设
,设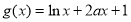 则:
则: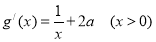
(ⅰ)当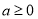 时:
时:
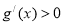 ,所以
,所以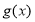 是增函数,不符合题意;
是增函数,不符合题意;
(ⅱ)当 时:由
时:由 得:
得: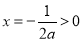
列表如下:
|
|
|
|
|
| 0 |
|
| ↗ | 极大值 | ↘ |
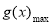 =
= ,解得:
,解得: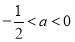
② 证明: 由①知: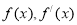 变化如下:
变化如下:
|
|
|
|
|
|
|
| 0 | + | 0 |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
由表可知: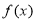 在
在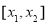 上为增函数,又
上为增函数,又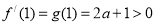 ,故
,故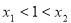
所以:
即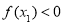 ,
,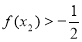 .
.
考点:导数的应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

















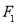 (-1,0),
(-1,0),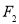 (1,0),过
(1,0),过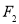 垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,
垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,
 MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.  (
(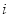 为虚数单位)在复平面上对应的点位于( )
为虚数单位)在复平面上对应的点位于( )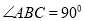 ,
,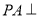 平面
平面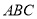 ,若
,若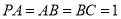 ,则四面体
,则四面体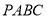 的外接球(顶点都在球面上)的表面积为( )
的外接球(顶点都在球面上)的表面积为( )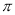 B.
B.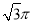 C.
C.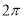 D.
D.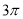
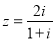 (
(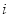 为虚数单位)在复平面上对应的点位于( )
为虚数单位)在复平面上对应的点位于( )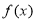 满足: (ⅰ)函数
满足: (ⅰ)函数 ; (ⅱ)对任意
; (ⅱ)对任意
 ;(ⅲ)
;(ⅲ)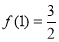 . 则下列命题中正确的是_____. (写出所有正确命题的序号)
. 则下列命题中正确的是_____. (写出所有正确命题的序号) 
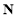 ,若
,若 ,则
,则 ;④ 对任意
;④ 对任意 ,有
,有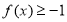 .
.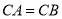 ,
, ,
,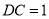 , 则三棱锥
, 则三棱锥 的体积为( )
的体积为( ) B.
B.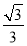 C.
C. D.
D.
 图象上点的横坐标扩大到原来的
图象上点的横坐标扩大到原来的 倍,纵坐标保持不变,再向左平移
倍,纵坐标保持不变,再向左平移 个单位得到如图所示函数的图象,则
个单位得到如图所示函数的图象,则 ,
, 可以为( )
可以为( )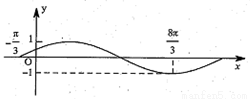
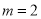 ,
,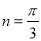 B.
B. ,
,
 ,
, ,
, 中,已知
中,已知 ,当
,当 时,
时,