题目内容
已知椭圆的焦点坐标为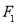 (-1,0),
(-1,0),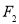 (1,0),过
(1,0),过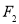 垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,
垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,

(1)求椭圆的方程;
(2)过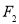 的直线l与椭圆交于不同的两点M、N,则△
的直线l与椭圆交于不同的两点M、N,则△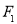 MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
(1) =1;(2)
=1;(2) π
π
【解析】
试题分析:(1)利用待定系数法即可求得椭圆方程为 =1;(2) 设M
=1;(2) 设M ,N
,N ,不妨
,不妨 >0,
>0,  <0,设△
<0,设△ MN的内切圆的径R,则△
MN的内切圆的径R,则△ MN的周长=4a=8,
MN的周长=4a=8, (MN+
(MN+ M+
M+ N)R=4R因此
N)R=4R因此 最大,R就最大,从而将问题转化为求
最大,R就最大,从而将问题转化为求 最大值,设直线l的方程为x=my+1,由
最大值,设直线l的方程为x=my+1,由 得
得 +6my-9=0,
+6my-9=0, ,
, ,则
,则 AB(
AB( )=
)= =
= ,再换元法及双钩函数的性质得到
,再换元法及双钩函数的性质得到 =
= 从而所求内切圆面积的最大值为
从而所求内切圆面积的最大值为 π.
π.
试题解析:(1) 设椭圆方程为 =1(a>b>0),由焦点坐标可得c=1 1由PQ|=3,可得
=1(a>b>0),由焦点坐标可得c=1 1由PQ|=3,可得 =3, 2分
=3, 2分
解得a=2,b= , 3分
, 3分
故椭圆方程为 =1 4分
=1 4分
(2) 设M ,N
,N ,不妨
,不妨 >0,
>0,  <0,设△
<0,设△ MN的内切圆的径R,
MN的内切圆的径R,
则△ MN的周长=4a=8,
MN的周长=4a=8, (MN+
(MN+ M+
M+ N)R=4R
N)R=4R
因此 最大,R就最大, 6分
最大,R就最大, 6分
 ,
,
由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由 得
得 +6my-9=0, 8分
+6my-9=0, 8分
得 ,
, ,
,
则 AB(
AB( )=
)= =
= , 9分
, 9分
令t= ,则t≥1,
,则t≥1,
则 , 10分
, 10分
令f(t)=3t+ ,则f′(t) =3-
,则f′(t) =3- ,
,
当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,
有f(t)≥f(1)=4,  ≤
≤ =3,
=3,
即当t=1,m=0时, ≤
≤ =3,
=3,  =4R,∴
=4R,∴ =
= ,
,
这时所求内切圆面积的最大值为 π.
π.
故直线l:x=1,△AMN内切圆面积的最大值为 π 13分
π 13分
考点:圆锥曲线与最值的综合应用

 阅读快车系列答案
阅读快车系列答案 满足
满足 ,
, (
( ),则
),则 的值为 .
的值为 .  在
在 上有意义,则实数
上有意义,则实数 的取值范围为
的取值范围为 B.
B.  C.
C.  D.
D. 
 的图像是
的图像是 

 对应的点位于
对应的点位于 ;②
;②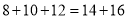 ;
;
 的方程x2-2x+a+b=0无实数根的概率为 ( )
的方程x2-2x+a+b=0无实数根的概率为 ( ) B.
B. C.
C. D.
D.
 ,则
,则 .
. 为常数,函数
为常数,函数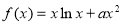 .
.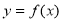 在
在 处的切线过点A
处的切线过点A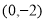 ,求实数
,求实数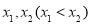 .
. ,②求证:
,②求证: .
.