题目内容
若函数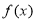 满足: (ⅰ)函数
满足: (ⅰ)函数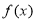 的定义域是
的定义域是 ; (ⅱ)对任意
; (ⅱ)对任意
 有
有 ;(ⅲ)
;(ⅲ)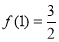 . 则下列命题中正确的是_____. (写出所有正确命题的序号)
. 则下列命题中正确的是_____. (写出所有正确命题的序号)
①函数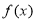 是奇函数;②函数
是奇函数;②函数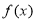 是偶函数;③对任意
是偶函数;③对任意
 ,若
,若 ,则
,则 ;④ 对任意
;④ 对任意 ,有
,有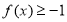 .
.
②③④
【解析】
试题分析:对任意
 有
有 ;令
;令 ,则
,则
 或
或 ,令
,令 ,则
,则 ,若
,若 则
则
 ,这与
,这与 矛盾,所以
矛盾,所以 ;令
;令 ,则
,则 ,
,
即: ,说明函数
,说明函数 是偶函数;③首先说明
是偶函数;③首先说明 ,因为
,因为 ,令
,令 ,则
,则 ,令
,令
则
 ,令
,令 ,则
,则
 ,则
,则
 ,可以发现
,可以发现 ,本结论可用数学归纳法给出证明,(1)当
,本结论可用数学归纳法给出证明,(1)当 时,
时, 成立,(2)假设当
成立,(2)假设当
 时成立,即
时成立,即 ,,那么当
,,那么当 时,令
时,令
 1,有
1,有

 ,
, ,则
,则
 ,即
,即 ,因此③对任意
,因此③对任意
 ,若
,若 ,则
,则 正确,
正确,
最后令 ,则
,则 ,则
,则 ,④正确;正确序号填②③④;
,④正确;正确序号填②③④;
考点:抽象函数

练习册系列答案
相关题目
 ;②
;② ;
;
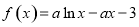 (
( ).
). 的单调性;
的单调性;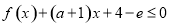 对任意
对任意 恒成立,求实数
恒成立,求实数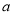 的取值范围(
的取值范围(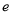 为自然常数);
为自然常数);
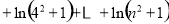

 (
( ,
, ).
).
 B.
B.
 D.
D.
 为常数,函数
为常数,函数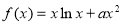 .
.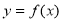 在
在 处的切线过点A
处的切线过点A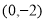 ,求实数
,求实数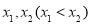 .
. ,②求证:
,②求证: .
. 在区间
在区间 上为增函数,则实数
上为增函数,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的内角A、B、C的对边分别为a、b、c,则“
的内角A、B、C的对边分别为a、b、c,则“ ”是“
”是“ ”的( )
”的( ) ,
, ,
, ,若函数
,若函数 恰有
恰有 个不同零点,则正实数
个不同零点,则正实数 的值为 .
的值为 . 中,底面
中,底面 是等腰梯形,
是等腰梯形, ,
, ,
, 是线段
是线段 的中点.
的中点. ;
; 垂直于平面
垂直于平面 ,求平面
,求平面 和平面
和平面