题目内容
20.已知x=($\frac{1}{5}$)${\;}^{-lo{g}_{5}7}$,则x=7.分析 由已知条件利用指数幂的运算法则和对数的性质能求出结果.
解答 解:由指数幂的运算法则和对数的性质得:
x=$(\frac{1}{5})^{-lo{g}_{5}7}$=${5}^{lo{g}_{5}7}$=7.
故答案为:7.
点评 本题考查对数值的求法,是基础题,解题时要认真审题,注意指数幂的运算法则和对数的性质的合理运用.

练习册系列答案
相关题目
15.对于?x1$∈(0,\frac{1}{2}]$,?x2$∈(0,\frac{1}{2}]$,4${\;}^{{x}_{1}}$<logax2恒成立,则a取值范围是( )
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
5.函数y=$\sqrt{-2{x}^{2}+x+3}$的值域为( )
| A. | [0,+∞) | B. | [0,$\sqrt{3}$] | C. | [0,$\frac{5\sqrt{2}}{4}$] | D. | (-∞,$\frac{5\sqrt{2}}{4}$] |
9.函数f(x)=${2}^{\sqrt{4+3x-{x}^{2}}}$的单调递减区间是( )
| A. | (-∞,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | [-1,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,4] |
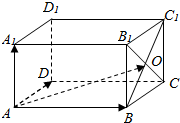 如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.