题目内容
10.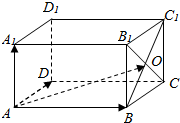 如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
分析 如图所示,可得:$\overrightarrow{AO}$=$\overrightarrow{AB}+\overrightarrow{BO}$,$\overrightarrow{BO}=\frac{1}{2}\overrightarrow{B{C}_{1}}$,$\overrightarrow{B{C}_{1}}=\overrightarrow{B{B}_{1}}+\overrightarrow{BC}$,$\overrightarrow{BC}=\overrightarrow{AD}$,$\overrightarrow{B{B}_{1}}=\overrightarrow{A{A}_{1}}$,代入利用向量的平行六面体法则即可得出.
解答 解:如图所示,可得:
$\overrightarrow{AO}$=$\overrightarrow{AB}+\overrightarrow{BO}$,$\overrightarrow{BO}=\frac{1}{2}\overrightarrow{B{C}_{1}}$,$\overrightarrow{B{C}_{1}}=\overrightarrow{B{B}_{1}}+\overrightarrow{BC}$,$\overrightarrow{BC}=\overrightarrow{AD}$,$\overrightarrow{B{B}_{1}}=\overrightarrow{A{A}_{1}}$,
∴$\overrightarrow{AO}=\overrightarrow{AB}$+$\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{A{A}_{1}})$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{A{A}_{1}}$,
又$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,
∴x=1,y=z=$\frac{1}{2}$.
则x+y+z=2.
故答案为:2.
点评 本题考查了向量的平行六面体法则、向量的三角形法则,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | y<z<x | B. | z<x<y | C. | z<y<x | D. | x<y<z |
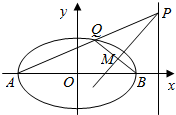 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?