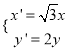题目内容
【题目】已知函数
.
（1）若
，
，求
的单调递减的概率；
（2）当
，
且为整数时，求二次函数有两个零点的概率.
【答案】（1）
；（2）
【解析】
（1）当
时，函数的单调性由一次项系数的符号来确定，根据其为减函数，从而得到一次项系数小于零，得到满足条件的
的取值范围，利用长度型几何概型概率公式求得结果；
（2）由函数有两个零点，得到其判别式大于零，写出所有满足
，
且为整数所对应的基本事件，找出满足条件的基本事件，利用古典概型概率公式求得结果.
（1）时，
时，
，
若
单调递减，
则
，
又，∴
时，单调递减，
∴单调递减的概率
.
（2）设二次函数有两个零点为事件
，
，
则
，
所有可能的结果为
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共有16种情况，
而满足
的结果有，，，，，，，，共8种，
所以
.
练习册系列答案
相关题目
【题目】某高级中学今年高一年级招收“国际班”学生
人，学校为这些学生开辟了直升海外一流大学的绿色通道，为了逐步提高这些学生与国际教育接轨的能力，将这人分为三个批次参加国际教育研修培训，在这三个批次的学生中男、女学生人数如下表：
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在这名学生中随机抽取
名，抽到第一批次、第二批次中女学生的概率分别是
.
（1）求
的值；
（2）为了检验研修的效果，现从三个批次中按分层抽样的方法抽取
名同学问卷调查，则三个批次被选取的人数分别是多少？
（3）若从第（2）小问选取的学生中随机选出两名学生进行访谈，求“参加访谈的两名同学至少有一个人来自第一批次”的概率.
