题目内容
如图11-19，在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=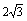
，M、N分别为AB、SB的中点
（1）证明：AC⊥SB；
（2）求二面角N-CM-B的大小。
（3）求点B到平面CMN的距离。
取AC中点O，连续OS、OB，∵SA=SC，AB=BC，∴AC⊥SO，AC⊥OB，又平面SAC⊥平面ABC，SO⊥AC，
∴SO⊥平面ABC，∴SO⊥BO。以OA、OB、OC分别为x轴、y轴、z轴建立空间直角坐标系如下图。
（3）由（1）、（2）得
为平面CMN的一个法向量。
∴点B到平面CMN的距离d=
练习册系列答案
相关题目
=
,且
，
，
}的通项公式，并用数学归纳法证明之.
与曲线
有且仅有一个公共点，则
的取值范围是 （ ）
B．
或
C．
D．
和
，必定存在平面
，使得（ ）
（B）
（D）
BC—A1B1C1中，∠ACB=90°，B1B=BC=CA=4，D1是A1B1中点E是BC1的中点，BD1交AB1于点F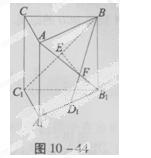
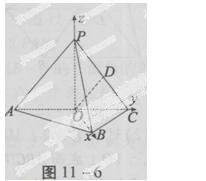
时，求直线PA与平面PBC所成角的大小；
合格的概率；
,…,根据以上式子可以猜想：
_________;