题目内容
15．抛物线y=ax2（a≠0）的焦点坐标为（ ）| A． | （0，$\frac{a}{4}$）或（0，-$\frac{a}{4}$） | B． | （0，$\frac{1}{4a}$）或（0，-$\frac{1}{4a}$） | C． | $（0，\frac{1}{4a}）$ | D． | $（\frac{1}{4a}，0）$ |
分析 先把抛物线方程整理成标准方程，进而根据抛物线的性质可得焦点坐标．
解答 解：当a＞0时，抛物线方程得x2=$\frac{1}{a}$y，抛物线的焦点在x轴正半轴，即p=$\frac{1}{2a}$，
由抛物线x2=2py（p＞0）的焦点为（0，$\frac{p}{2}$），
所求焦点坐标为（0，$\frac{1}{4a}$）．
当a＜0时，同理可知：焦点坐标为（0，$\frac{1}{4a}$）．
综上可知：焦点坐标为（0，$\frac{1}{4a}$）．
故选：C．
点评 本题主要考查了抛物线的标准方程、抛物线的性质．属基础题．
练习册系列答案
相关题目
5．设U=R，M={y|y=2x+1，-$\frac{1}{2}$≤x≤$\frac{1}{2}$}，N={x|y=lg（x2+3x）}，则（∁UM）∩N=（ ）
| A． | （-∞，-3]∪（2，+∞） | B． | （-∞，-3）∪（0，+∞） | C． | （-∞，-3）∪（2，+∞） | D． | （-∞，0）∪（2，+∞） |
6．设$\overrightarrow{a}$，$\overrightarrow{b}$，是任意的非零平面向量，且相互不共线，则下列正确的是（ ）
| A． | 若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，且$\overrightarrow{a}$，$\overrightarrow{b}$同向，则$\overrightarrow{a}$＞$\overrightarrow{b}$ | |
| B． | |$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | |
| C． | |$\overrightarrow{a}$•$\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | |
| D． | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
3．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1，F2为椭圆的左．右焦点，M是椭圆上任一点，若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$的取值范围为[-3，3]，则椭圆方程为（ ）
| A． | $\frac{x^2}{9}+\frac{y^2}{3}=1$ | B． | $\frac{x^2}{6}+\frac{y^2}{3}=1$ | C． | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{4}$+y2=1 |
20．下列命题正确的是（ ）
| A． | 若ac＞bc，则a＞b | B． | 若a＜b，则ac2＜bc2 | ||
| C． | 若$\frac{1}{a}$＜$\frac{1}{b}$＜0，则a＞b | D． | 若a＞b，c＞d，则a-c＞b-d |
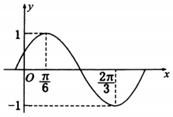函数f（x）=Asin（ωx+φ）（A＞0，ω，0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．