��Ŀ����
17���۲����е�ʽ����cos2��=2cos2��-1��
��cos4��=8cos4��-8cos2��+1��
��cos6��=32cos6��-48cos4��+18cos2��-1��
��cos8��=128cos8��-256cos6��+160cos4��-32cos2��+1��
��cos10��=mcos10��-1280cos8��+1120cos6��+ncos4��+pcos2��-1��
�����Ʋ⣬m+n-p=62��
���� �۲�5����ʽ��ߵĦ���ϵ�����Լ���ʽ�ұ߸���ϵ�����ص㣬m��n��p�ı仯���ƣ����ѹ��ɳ��������ı仯���ɣ������m��n��p��ֵ��������𰸣�
��� �⣺�������ʽ�ɵã���һ���ϵ���ֱ�Ϊ��
2=21��8=23��32=25������128=27������m=29=512��
��ÿһ�е����ڶ����ϵ������������֣�1��2��-2��4��3��6��-4��8��5��10���������p=50��
����ÿ�е�ϵ���Ͷ�Ϊ1���ɵ�n=-400��
����m+n-p=512-400-50=62��
�ʴ�Ϊ��62��
���� ���⿼������������ѵ��Ǹ����ܹ��ҳ���֮������ڹ��ɣ�����۲졢���������ɵ��������ǻ����⣮

��ϰ��ϵ�д�
�����Ŀ
12����֪����M={x|-1��x��1}��N={x|x2��2��x��Z}��������
| A�� | M⊆N | B�� | N⊆M | C�� | M��N={0} | D�� | M��N=N |
13����֪450�㣼����510�㣬��$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cos2��}}$��ֵ�ǣ�������
| A�� | -sin$\frac{��}{2}$ | B�� | cos$\frac{��}{2}$ | C�� | sin$\frac{��}{2}$ | D�� | -cos$\frac{��}{2}$ |
6����֪����X={x��Z|x2-x-6��0}��Y={y|y=1-x2��x��R}����X��Y=��������
| A�� | {-3��-2��-1��0} | B�� | {-2��-1��0} | C�� | {-3��-2��-1��0��1} | D�� | {-2��-1��0��1} |
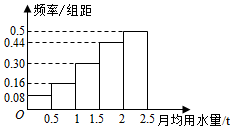 ��ͼΪijС��100Ϊ����2015����ƽ����ˮ������λ��t����Ƶ�ʷֲ�ֱ��ͼ��һ���֣��ݴ˿�����100λ������ƽ����ˮ������λ��Ϊ2.02�֣�
��ͼΪijС��100Ϊ����2015����ƽ����ˮ������λ��t����Ƶ�ʷֲ�ֱ��ͼ��һ���֣��ݴ˿�����100λ������ƽ����ˮ������λ��Ϊ2.02�֣�