题目内容
已知正方体ABCD-A1B1C1D1中，E、F分别为C1D1，B1C1的中点，AC∩BD=P，A1C1∩EF=Q，求证：
（1）D、B、F、E四点共面；
（2）若A1C交平面DBFE于R点，则P、Q、R三点共线．
（1）D、B、F、E四点共面；
（2）若A1C交平面DBFE于R点，则P、Q、R三点共线．
考点：空间中直线与平面之间的位置关系
专题：
分析：（1）由已知得EF∥D1B1，BB1∥DD1、BB1=DD1，从而BB1D1D是平行四边形，从而EF∥DB，由此能证明D、B、F、E共面．
（2）由已知得EF是平面AA1C1C和平面DBFE的交线，R是EF是平面AA1C1C和平面DBFE的一个公共点，由此能证明P、Q、R三点共线．
（2）由已知得EF是平面AA1C1C和平面DBFE的交线，R是EF是平面AA1C1C和平面DBFE的一个公共点，由此能证明P、Q、R三点共线．
解答：
证明：（1）∵E、F分别为C1D1，B1C1的中点，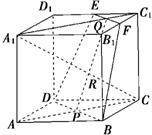
∴EF是△B1C1D1的中位线，∴EF∥D1B1，
∵ABCD-A1B1C1D1是正方体，∴BB1∥DD1、BB1=DD1，
∴BB1D1D是平行四边形，
∴DB∥DB1，∴EF∥D1B1，
∴EF∥DB，∴D、B、F、E共面．
（2）∵AC∩BD=P，A1C1∩EF=Q，
∴EF是平面AA1C1C和平面DBFE的交线，
∵A1C交平面DBFE于R点，
∴R是EF是平面AA1C1C和平面DBFE的一个公共点，
∵两相交平面的所有公共点都在这两平面的交线上，
∴P、Q、R三点共线．
∴EF是△B1C1D1的中位线，∴EF∥D1B1，
∵ABCD-A1B1C1D1是正方体，∴BB1∥DD1、BB1=DD1，
∴BB1D1D是平行四边形，
∴DB∥DB1，∴EF∥D1B1，
∴EF∥DB，∴D、B、F、E共面．
（2）∵AC∩BD=P，A1C1∩EF=Q，
∴EF是平面AA1C1C和平面DBFE的交线，
∵A1C交平面DBFE于R点，
∴R是EF是平面AA1C1C和平面DBFE的一个公共点，
∵两相交平面的所有公共点都在这两平面的交线上，
∴P、Q、R三点共线．
点评：本题考查四点共面的证明，考查三点共线的证明，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
设f（x）为奇函数，且在（-∞，0）内是减函数，f（3）=0，则x f（x）＜0的解集为（ ）
| A、（-3，0）∪（3，+∞） |
| B、（-∞，-3）∪（0，3 ） |
| C、（-3，0）∪（0，3 ） |
| D、（-∞，-3）∪（3，+∞） |
计算：i（i+1）=（ ）
| A、i+1 | B、i-1 |
| C、-i+1 | D、-i-1 |
已知一个空间几何体的三视图如图所示，其中正视图、侧视图都是由半圆和矩形组成，根据图中标出的尺寸，可得这个几何体的体积是四面体S-ABC中，已知SA⊥AB，AB⊥BC，|
|=3，|
|=4，|
|=5，|
|=
，则二面角S-AB-C的大小为（ ）
| SA |
| AB |
| BC |
| SC |
| 35 |
A、
| ||
B、
| ||
C、
| ||
D、
|