题目内容
6.点P(4,0)关于直线5x+4y+21=0的对称点的坐标是(-6,-8).分析 设出对称的点的坐标(a,b),利用点P与对称的点的连线与对称轴垂直,以及点P与对称的点的连线的中点在对称轴上,解出对称点的坐标.
解答 解:设点P(4,0)关于直线5x+4y+21=0的对称点P′的坐标(a,b),
∴$\frac{b}{a-4}$•(-$\frac{5}{4}$)=-1①
且5•$\frac{a+4}{2}$+4•$\frac{b}{2}$+21=0②,
解得a=-6,b=-8,
∴点P′的坐标为(-6,-8).
故答案为:(-6,-8).
点评 本题考查求一个点关于某一条直线的对称点的坐标的求法,利用垂直及中点在轴上两个条件解出对称点的坐标.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.已知 sinα>0,cosα<0,则角α的终边在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
14.已知sin($\frac{π}{6}$-α)=$\frac{1}{3}$,则$cos[{2(\frac{π}{3}+α)}]$的值是( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
11.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为8,23,27,43,则这四个社区驾驶员的总人数N为( )
| A. | 101 | B. | 808 | C. | 1212 | D. | 2012 |
18.已知随机变量ξ服从正态分布N(2016,σ2),则P(ξ<2016)等于( )
| A. | $\frac{1}{1008}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
15.已知函数f(x)=ax2-(a+2)x+lnx在(0,1)内存在极小值,则实数a的取值范围是( )
| A. | (-∞,2) | B. | (1,2) | C. | (1,+∞) | D. | (1,2)∪(2,+∞) |
16.已知集合A={-1,0,1,2,3,4,5},B={b|b=n2-1,n∈Z},则A∩B=( )
| A. | {-1,3} | B. | {0,3} | C. | {-1,0,3} | D. | {-1,0,3,5} |
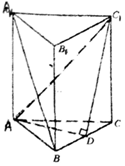 正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.
正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.