题目内容
1.已知函数$f(x)={a^2}x-\frac{1}{x}-2aln(ax)+\frac{1}{2}$,f'(x)为其导函数.(1)设$g(x)=f(x)+\frac{1}{x}$,求函数g(x)的单调区间;
(2)若a>0,设A(x1,f(x1)),B(x2,f(x2))为函数f(x)图象上不同的两点,且满足f(x1)+f(x2)=1,设线段AB中点的横坐标为x0,证明:ax0>1.
分析 (1)求出函数的导数,通过讨论a的范围求出函数的单调区间即可;
(2)问题转化为证明$1-f({x_2})>f(\frac{2}{a}-{x_2})$(*)令$F(x)=f(\frac{2}{a}-x)+f(x)-1={a^2}(\frac{2}{a}-x)-\frac{1}{{\frac{2}{a}-x}}-2aln(2-ax)+{a^2}x-\frac{1}{x}-2alnax$,法一:根据函数的单调性证明即可;法二:结合函数的图象判断即可.
解答 (1)解:$g(x)={a^2}x-2alnax+\frac{1}{2}$,$g'(x)={a^2}-\frac{2a}{x}=\frac{a(ax-2)}{x}$,
①a>0时,g(x)定义域为(0,+∞),
在$(0,\frac{2}{a})$上g'(x)<0,故g(x)在$(0,\frac{2}{a})$上单调递减;
在$(\frac{2}{a},+∞)$上g'(x)>0,故g(x)在$(\frac{2}{a},+∞)$上单调递增.
②a<0时,g(x)定义域为(-∞,0),在
$(-∞,\frac{2}{a})$上g'(x)>0,故g(x)在$(-∞,\frac{2}{a})$上单调递增;
在$(\frac{2}{a},0)$上g'(x)<0,故g(x)在$(\frac{2}{a},0)$上单调递减.
(2)证明:法一:$a{x_0}>1?\frac{{{x_1}+{x_2}}}{2}>\frac{1}{a}?{x_1}>\frac{2}{a}-{x_2}$$f'(x)={a^2}+\frac{1}{x^2}-\frac{2a}{x}={(\frac{1}{x}-a)^2}≥0$,
故f(x)在定义域(0,+∞)上单调递增.
只需证:$f({x_1})>f(\frac{2}{a}-{x_2})$,即证$1-f({x_2})>f(\frac{2}{a}-{x_2})$(*)
注意到$f({x_1})+f({x_2})=1,f(\frac{1}{a})=\frac{1}{2}$,不妨设$0<{x_1}<\frac{1}{a}<{x_2}$.
令$F(x)=f(\frac{2}{a}-x)+f(x)-1={a^2}(\frac{2}{a}-x)-\frac{1}{{\frac{2}{a}-x}}-2aln(2-ax)+{a^2}x-\frac{1}{x}-2alnax$,
则$F'(x)=\frac{1}{x^2}-\frac{a^2}{{{{(2-ax)}^2}}}-\frac{2a}{x}+\frac{{2{a^2}}}{2-ax}=-\frac{{4{{(ax-1)}^3}}}{{{x^2}{{(2-ax)}^2}}}≤0$,
$?x≥\frac{1}{a}$,从而F(x)在$[\frac{1}{a},+∞)$上单减,
故$F({x_2})<F(\frac{1}{a})=0$,即得(*)式.
法而二:$f'(x)={a^2}+\frac{1}{x^2}-\frac{2a}{x}={(\frac{1}{x}-a)^2}≥0$故f(x)在定义域(0,+∞)上单调递增.
注意到$f'(\frac{1}{a})=0$且$f(\frac{1}{a})=\frac{1}{2}$.
设$h(x)=\frac{a^4}{3}{(x-\frac{1}{a})^3}+\frac{1}{2}$,则h(x)单调递增且图象关于$(\frac{1}{a},\frac{1}{2})$中心对称.
构造函数$g(x)=h(x)-f(x)=\frac{a^4}{3}{(x-\frac{1}{a})^3}-{a^2}x+\frac{1}{x}+2alnax$,
$g'(x)={a^4}{(x-\frac{1}{a})^2}-{a^2}-\frac{1}{x^2}+\frac{2a}{x}=\frac{{{{(ax-1)}^2}({a^2}{x^2}-1)}}{x^2}$,
当$x>\frac{1}{a}$时,g'(x)>0,g(x)单增;当$0<x<\frac{1}{a}$时,g'(x)<0,g(x)单减,
故$g(x)≥g(\frac{1}{a})=0$,且等号仅在$\frac{1}{a}$处取到.所以h(x)与f(x)图象关系如下:
取h(x3)=f(x1),h(x4)=f(x2),
则显然有x1>x3,x2>x4,从而x1+x2>x3+x4,
另外由三次函数h(x)的中心对称性可知${x_3}+{x_4}=\frac{2}{a}$,
则有 ${x_1}+{x_2}>\frac{2}{a}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想、数形结合思想,是一道综合题.

| A. | 5 | B. | 3 | C. | 6 | D. | 7 |
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 5 | 4 | 3 | 2 | 4 | 2 |
| A. | 0.70 | B. | 0.60 | C. | 0.45 | D. | 0.35 |
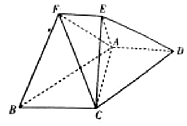 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.