题目内容
2.将函数f(x)=sinωx(ω是正整数)的图象向右平移$\frac{π}{6}$个单位,所得曲线在区间$(\frac{4π}{3},\frac{3π}{2})$内单调递增,则ω的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由题意可得可得2kπ-$\frac{π}{2}$≤ω($\frac{4π}{3}$-$\frac{π}{6}$)<ω($\frac{3π}{2}$-$\frac{π}{6}$)≤2kπ+$\frac{π}{2}$,k∈Z.解得$\frac{12k}{7}$-$\frac{3}{7}$≤ω≤$\frac{3}{2}$k+$\frac{3}{8}$,由此求得可得正整数ω的最大值.
解答 解:将函数f(x)=sinωx(ω是正整数)的图象向右平移$\frac{π}{6}$个单位,
可得y=sinω(x-$\frac{π}{6}$)的图象.
∵所得曲线在区间$(\frac{4π}{3},\frac{3π}{2})$内单调递增,可得2kπ-$\frac{π}{2}$≤ω($\frac{4π}{3}$-$\frac{π}{6}$)<ω($\frac{3π}{2}$-$\frac{π}{6}$)≤2kπ+$\frac{π}{2}$,k∈Z.
求得$\frac{12k}{7}$-$\frac{3}{7}$≤ω≤$\frac{3}{2}$k+$\frac{3}{8}$,令k=2,可得正整数ω的最大值为3,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性和单调性,属于中档题.

练习册系列答案
相关题目
15.设函数f(x)=lnx-2x+6,则f(x)零点的个数为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
17.“cos2α=0”是“sinα=cosα”的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
13.已知一组数据a、b、9、10、11的平均数为10,方差为2,则|a-b|=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
10.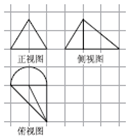 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )| A. | 1+$\frac{2π}{3}$ | B. | $\frac{4}{3}$+$\frac{2π}{3}$ | C. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{6}$ | D. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{3}$ |