题目内容
10.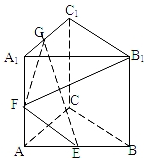 正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )
正三棱柱ABC-A1B1C1,E,F,G为 AB,AA1,A1C1的中点,则B1F与面GEF成角的正弦值( )| A. | $\frac{5}{6}$ | B. | $\frac{3}{5}$ | C. | $\frac{3\sqrt{3}}{10}$ | D. | $\frac{3\sqrt{6}}{10}$ |
分析 利用等体积,计算B1到平面EFG距离,再利用正弦函数,可求B1F 与面GEF成角的正弦值.
解答 解:取A1B1中点M,连接EM,则EM∥AA1,EM⊥平面ABC,连接GM
∵G为A1C1的中点,棱长为
∴GM=$\frac{1}{2}$B1C1=1,A1G═A1F=1,FG=$\sqrt{2}$,FE=$\sqrt{2}$,GE=$\sqrt{5}$,
在平面EFG上作FN⊥GE,则∵△GFE是等腰三角形,∴FN=$\frac{\sqrt{3}}{2}$,
∴S△GEF=$\frac{1}{2}$GE×FN=$\frac{\sqrt{15}}{4}$,
${S}_{△EF{B}_{1}}$=${S}_{正方形AB{B}_{1}{A}_{1}}$-${S}_{△{A}_{1}{B}_{1}F}$-${S}_{△B{B}_{1}E}$-S△AFE=$\frac{3}{2}$,
作GH⊥A1B1,GH=$\frac{\sqrt{3}}{2}$,
∴${V}_{三棱锥G-FE{B}_{1}}$=$\frac{1}{3}$${S}_{△EF{B}_{1}}$×GH=$\frac{\sqrt{3}}{4}$,
设B1到平面EFG距离为h,则${V}_{三棱锥{B}_{1}-EFG}$=$\frac{h}{3}$S△GEF=$\frac{\sqrt{15}h}{12}$,
∵${V}_{三棱锥G-FE{B}_{1}}$=${V}_{三棱锥{B}_{1}-EFG}$,
∴$\frac{\sqrt{15}h}{12}$=$\frac{\sqrt{3}}{4}$,
∴h=$\frac{3\sqrt{5}}{5}$,
设B1F与平面GEF成角为θ,
∵B1F=$\sqrt{5}$
∴sinθ=$\frac{h}{{B}_{1}F}$=$\frac{3}{5}$,
∴B1F与面GEF所成的角的正弦值为$\frac{3}{5}$.
故选B.
点评 本题考查线面角,考查三棱锥的体积计算,考查转化思想,解题的关键是利用等体积计算点到面的距离.

| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
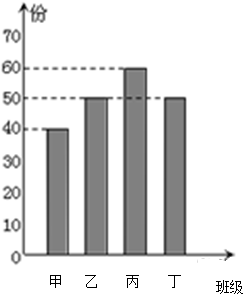 某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 甲班 | 乙班 | 丙班 | 丁班 | |
| 满意 | 50% | 80% | 100% | 60% |
| 一般 | 25% | 0 | 0 | 0 |
| 不满意 | 25% | 20% | 0 | 40% |
(2)若需从调查问卷被选中且填写不满意的学生中再选2人进行访谈,求这两人中至少有一人是丁班学生的概率.
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
 .
. 的定义域;
的定义域; ,求
,求 的值.
的值.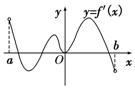 已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )
已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )