题目内容
7.在空间直角坐标系中,已知A(3,0,a),B(0,3,-2),C(1,1,-1),若平面ABC过坐标原点,则a=-1.分析 利用空间向量共面定理,列出方程,求解即可.
解答 解:在空间直角坐标系中,已知A(3,0,a),B(0,3,-2),C(1,1,-1),若平面ABC过坐标原点,
可得$\overrightarrow{OA}$=$λ\overrightarrow{OB}$$+μ\overrightarrow{OC}$,
即:(3,0,a)=λ(0,3,-2)+μ(1,1,-1),
可得$\left\{\begin{array}{l}{3=μ}\\{3λ+μ=0}\\{a=-2λ-μ}\end{array}\right.$,
解得$\left\{\begin{array}{l}{μ=3}\\{λ=-1}\\{a=-1}\end{array}\right.$.
故答案为:-1.
点评 本题考查空间向量共面定理的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
19.已知条件p:|x+1|<2,条件q:3x<3,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知A,B,P是双曲线mx2-ny2=1(m>0,n>0)上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率积为$\frac{2}{3}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
16.执行如图所示的程序框图,若输出的结果为3,则输入的实数x的值是( )
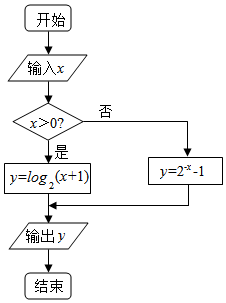

| A. | -2 | B. | 2 | C. | 7 | D. | -2或7 |