题目内容
16.执行如图所示的程序框图,若输出的结果为3,则输入的实数x的值是( )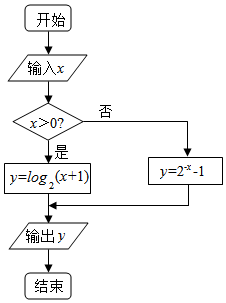
| A. | -2 | B. | 2 | C. | 7 | D. | -2或7 |
分析 根据题中程序框图的含义,得到分段函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{{log}_{2}(x+1),x>0}\end{array}\right.$,
再令f(x)=3,求出x的值即可.
解答 解:根据题意,该执行该程序框图的结果是
当x≤0时,输出函数y=2-x-1;
当x>0时,输出函数y=log2(x+1);
因此,当输出结果为3时,
①若x≤0,则y=2-x-1=3,解得x=-2;
②若x>0,则log2(x+1)=8,解得x=7;
综上,可输入的实数x的值是-2或7.
故选:D.
点评 本题考查了程序框图的应用问题,着重考查了对分段函数和程序框图的理解与应用问题,是基础题.

练习册系列答案
相关题目
7.函数f(x)=2cos(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则f(0)的值( )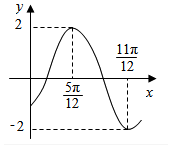

| A. | $-\frac{3}{2}$ | B. | -1 | C. | $-\sqrt{2}$ | D. | $-\sqrt{3}$ |
1.已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1且垂直于实轴的直线与双曲线的两条渐近线分别相交于A、B两点,若坐标原点O恰为△ABF2的垂心(三角形三条高的交点),则双曲线的离心率为( )
| A. | $\frac{\sqrt{21}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
4.直线l:y=kx与曲线C:y=x3-4x2+3x顺次相交于A,B,C三点,若|AB|=|BC|,则k=( )
| A. | -5 | B. | -$\frac{5}{9}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |