题目内容
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛
AMPN，要求B点在AM上，D点在AN上，且对角线MN过C点，已知AB＝3米，AD＝2米．
(1)要使矩形AMPN的面积大于32平方米，则DN的长应在什么范围内？
(2)当DN的长为多少时，矩形花坛AMPN的面积最小？并求出最小值．
解 (1)设DN的长为x (x>0)米，则AN＝(x＋2)米
∵
＝
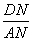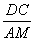，∴AM＝
，
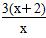∴SAMPN＝AN·AM＝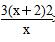
由SAMPN>32，得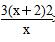>32，又x>0，
得3x2－20x＋12>0，解得：0<x<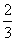
或x>6，
即DN长的取值范围是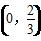
∪(6，＋∞)．
(2)矩形花坛AMPN的面积为
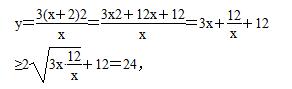当且仅当3x＝
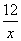，即x＝2时，矩形花坛AMPN的面积取得最小值24.
故DN的长为2米时，矩形AMPN的面积最小，最小值为24平方米．
练习册系列答案
相关题目
的值是________．
时，s(t)<3d2成立，则d的取值范围为__________．
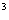－3ax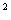
＋3bx的图象与直线12x＋y－1＝0相切于点(1，－
11).
≥1，x∈R}，B＝{x|x2－2x－m<0}，
∩B＝{x|－1<x<4}，求实数m的值．
时，求(∁UB)∩A；