题目内容
【题目】
(1)求 ![]() 的值;
的值;
(2)设m , n![]() N* , n≥m , 求证:
N* , n≥m , 求证:![]() .
.
【答案】
(1)
解: ![]()
(2)
解:对任意的 ![]() ,
,
① 当 ![]() 时,左边
时,左边 ![]() ,右边
,右边 ![]() ,等式成立,
,等式成立,
② 假设 ![]() 时命题成立,
时命题成立,
即 ![]() ,
,
当 ![]() 时,
时,
左边= ![]()
![]() ,
,
右边 ![]() ,
,
而 ![]() ,
,
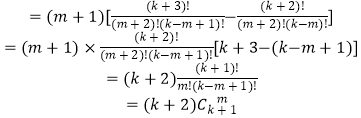
因此 ![]() ,
,
因此左边=右边,
因此 ![]() 时命题也成立,
时命题也成立,
综合①②可得命题对任意 ![]() 均成立.
均成立.
另解:因为 ![]() ,所以
,所以
左边 ![]()
![]()
又由 ![]() ,知
,知 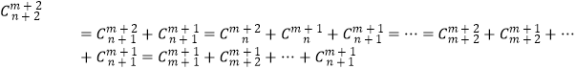 ,
,
所以,左边 ![]() 右边.
右边.
【解析】(1)由已知直接利用组合公式能求出7 ![]() 的值.(2)对任意m∈N* , 当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C
的值.(2)对任意m∈N* , 当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C ![]() +(m+2)C
+(m+2)C ![]() +(m+3)C
+(m+3)C ![]() +…+nC
+…+nC ![]() +(n+1)C
+(n+1)C ![]() =(m+1)C
=(m+1)C ![]() .
.
【考点精析】通过灵活运用组合与组合数的公式,掌握从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合即可以解答此题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目