题目内容
【题目】已知函数
的最小值为
．
⑴设
，求证： 
在
上单调递增；
⑵求证： 
；
⑶求函数
的最小值．
【答案】⑴见解析⑵见解析⑶见解析
【解析】试题分析：（1）先求导求出
，再求导，利用导数的符号变换得到函数
的单调区间；（2）由⑴可知
在
上单调递增，再利用零点存在定理及函数的单调性进行求解；（3）分离参数，合理构造，利用导数研究函数的最值.
试题解析：⑴
∵
∴
在
上单调递增
⑵由⑴可知
在
上单调递增
∵
∴
存在唯一的零点，设为
，则
且
当
时， 
；当
时， 
从而
在
上单调递增，在
上单调递减
所以
的最小值
∵
∴
∴
∴
（当且仅当
时取等号）
∵
∴
（第二问也可证明
，从而得到
）
⑶
同⑴方法可证得
在
上单调递增
∵
∴
∴
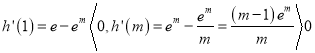
存在唯一的零点，设为
，则
且
所以
的最小值为
∵
∴
∴
，即
由⑵可知
∴
=
∵
在
上单调递增
∴
所以
的最小值为
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
