题目内容
17.函数y=$\frac{1}{3}{x^3}-{x^2}$-3x+9的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先利用导数判断函数的单调性,然后说明f(x)存在零点,由此即可得到答案.
解答 解:f′(x)=x2-2x-3=(x+1)(x-3),令(x+1)(x-3)=0,可得x=-1,x=3,
函数有两个极值点,并且f(-1)=$-\frac{1}{3}-1+3+9$>0,f(3)=9-9-9+9=0,
x∈(-∞,-1),x∈(3,+∞),f′(x)>0,x∈(-1,3),f′(x)<0,
x=-1函数取得极大值,x=3时,函数取得极小值,
所以f(x)的零点个数为2.
故选:C.
点评 本题的考点是函数零点,用导函数判断函数单调性,属中档题.

练习册系列答案
相关题目
5.设i为虚数单位,复数$\frac{a+2i}{1+i}$为纯虚数,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
2.在△ABC中,a,b,c分别为三个内角A,B,C的对边,若a=2,b=1,B=29°,则此三角形解的情况是( )
| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 有无数解 |
7.若集合A={x|3x-x2>0},集合B={x|x<1},则A∩(∁UB)等于( )
| A. | (-3,1] | B. | (-∞,1] | C. | [1,3) | D. | (3,+∞) |
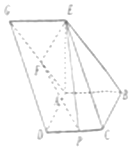 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.