题目内容
16.设函数f(x)=(x-a)2lnx,a∈R.(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)-4e2只有一个零点,求实数a的取值范围.
分析 (Ⅰ)求出导函数,另一回事的极值为0,求解a,然后验证即可.
(Ⅱ)解法1:方程f(x)=4e2只有一个根,转化为曲线f(x)与直线y=4e2只有一个公共点.设$h(x)=2lnx+1-\frac{a}{x}$,通过①当a≤0时,②当0<a≤1时,③当a>1时,判断函数的单调性,求出极大值,转化为$f({x_0})<4{e^2}$,即${({x_0}-a)^2}ln{x_0}<4{e^2}$,
所以${x_0}^2{ln^3}{x_0}<{e^2}$,然后推出a的范围.
解答 解:(Ⅰ)函数f(x)=(x-a)2lnx,a∈R.
$f'(x)=(x-a)(2lnx+1-\frac{a}{x})$,----------------(2分)
由x=e是f(x)的极值点,得$f'(e)=({e-a})({3-\frac{a}{e}})=0$,解得a=e或a=3e,---------(3分)
经检验,符合题意,所以a=e或a=3e;-----------------------(4分)
(Ⅱ)由已知得方程f(x)=4e2只有一个根,
即曲线f(x)与直线y=4e2只有一个公共点.
易知f(x)∈(-∞,+∞),设$h(x)=2lnx+1-\frac{a}{x}$,-----------------(5分)
①当a≤0时,易知函数f(x)在(0,+∞)上是单调递增的,满足题意;-------------(6分)
②当0<a≤1时,易知h(x)是单调递增的,又h(a)=2lna<0,h(1)=1-a≥0,
∴?x0∈(a,1),h(x0)=0,
当0<x<a时,$f'(x)=(x-a)(2lnx+1-\frac{a}{x})$>0,∴f(x)在(0,a)上单调递增,
同理f(x)在(a,x0)上单调递减,在(x0,+∞)上单调递增,
又极大值f(a)=0,所以曲线f(x) 满足题意;-----------------------(8分)
③当a>1时,h(1)=1-a<0,h(a)=2lna>0,
∴?x0∈(1,a),h(x0)=0,即$2ln{x_0}+1-\frac{a}{x_0}=0$,得a-x0=2x0lnx0,
可得f(x) 在(0,x0)上单调递增,在(x0,a)上单调递减,在(a,+∞)上单调递增,
又f(a)=0,若要曲线f(x) 满足题意,只需$f({x_0})<4{e^2}$,即${({x_0}-a)^2}ln{x_0}<4{e^2}$,
所以${x_0}^2{ln^3}{x_0}<{e^2}$,由x0>1知g(x)=x2ln3x>0,且在[1,+∞)上单调递增,
由g(e)=e2,得1<x0<e,因为a=x0+2x0lnx0在[1,+∞)上单调递增,
所以1<a<3e;------------------------------------(11分)
综上知,a∈(-∞,3e).------------------------------------(12分)
点评 本题考查函数的导数的应用,函数的极值以及函数的单调性,构造法的应用,转化思想以及分类讨论思想的应用,难度比较大.

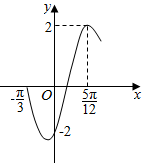 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )| A. | $2\;,\;-\frac{π}{3}$ | B. | $2\;,\;-\frac{π}{6}$ | C. | $4\;,\;-\frac{π}{6}$ | D. | $4\;,\;\frac{π}{3}$ |
| 零件数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(min) | 26 | 39 | 49 | 54 |
| A. | 63.6min | B. | 65.5min | C. | 67.7min | D. | 72.0min |
| 组别 | 分组 | 频数 | 频率 |
| 1 | [50,60) | a | 0.08 |
| 2 | [60,70) | 15 | 0.3 |
| 3 | [70,80) | 21 | c |
| 4 | [80,90) | 6 | 0.12 |
| 5 | [90,100) | 4 | 0.08 |
| 合计 | b | 1.00 | |
(2)若分数字80(含80分)以上表示对“网上银行、手机银行办理业务免费政策”非常满意,其中分数在90(含有90分)以上表示“十分满意”,现从被抽取的“”非常满意人群中随机抽取2人,求至少一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数.