题目内容
16. 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.求证:
(1)A1C⊥BD;
(2)平面AB1D1∥平面BC1D.
分析 (1)要证A1C⊥BD,只需证DB⊥面A1ACC1即可,
(2)利用线面平行的判定证明.
解答  (1)证明:在正方体ABCD-A1B1C1D1中,则有DB⊥AC,DB⊥AA1,
(1)证明:在正方体ABCD-A1B1C1D1中,则有DB⊥AC,DB⊥AA1,
且AA1∩AC=A,∴DB⊥面AA1C1C,
∵A1C?面AA1C1C,
∴A1C⊥BD;
(2)∵$\left\{\begin{array}{l}{{D}_{1}{C}_{1}=AB}\\{{D}_{1}{C}_{1}∥AB}\end{array}\right.$∴四边形ABC1D1是平行四边形,∴AD1∥BC1,
又∵DB∥B1D1,AD1?面AD1B1,B1D1?面AD1B1,
BD?面DBC1,BC1?面DBC1,且AD1 ∩D1B1=D1.
∴平面AB1D1∥平面BC1D.
点评 本题考查了空间线线,线面,面面位置关系,属于中档题.

练习册系列答案
相关题目
4.阅读如图所示的程序框图,则输出的S的值是( )


| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |
8.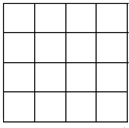 将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
 将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )| A. | 288 | B. | 144 | C. | 576 | D. | 96 |
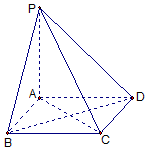 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.