题目内容
6.已知非零平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$=3,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{c}$|=2,则向量$\overrightarrow{a}$在向量$\overrightarrow{c}$方向上的投影为$\frac{3}{2}$,$\overrightarrow{a}$•$\overrightarrow{b}$的最小值为$\frac{5}{4}$.分析 根据条件容易求出向量$\overrightarrow{a}$在$\overrightarrow{c}$方向上的投影为$\frac{3}{2}$,并且根据条件可得到$(\overrightarrow{a}-\overrightarrow{b})⊥\overrightarrow{c}$,从而可设$\overrightarrow{a}-\overrightarrow{b}=(0,2),\overrightarrow{c}=(2,0)$,可设$\overrightarrow{a}=(x,y),\overrightarrow{b}=(x,2-y)$,由$\overrightarrow{a}•\overrightarrow{c}=3$便可得出x=$\frac{3}{2}$,从而$\overrightarrow{a}=(\frac{3}{2},y),\overrightarrow{b}=(\frac{3}{2},y-2)$,这便可得到$\overrightarrow{a}•\overrightarrow{b}=\frac{9}{4}+{y}^{2}-2y$,配方便可求出$\overrightarrow{a}•\overrightarrow{b}$的最小值.
解答 解:向量$\overrightarrow{a}$在向量$\overrightarrow{c}$方向上的投影为:$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{c}|}=\frac{3}{2}$;
由$\overrightarrow{a}•\overrightarrow{c}=\overrightarrow{b}•\overrightarrow{c}$得,$(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{c}=0$;
∴$(\overrightarrow{a}-\overrightarrow{b})⊥\overrightarrow{c}$;
∵$|\overrightarrow{a}-\overrightarrow{b}|=|\overrightarrow{c}|=2$;
∴设$\overrightarrow{a}-\overrightarrow{b}=(0,2),\overrightarrow{c}=(2,0)$,设$\overrightarrow{a}=(x,y)$,则$\overrightarrow{b}=(x,y-2)$;
∴$\overrightarrow{a}•\overrightarrow{c}=2x=3$;
∴$x=\frac{3}{2}$;
∴$\overrightarrow{a}=(\frac{3}{2},y),\overrightarrow{b}=(\frac{3}{2},y-2)$;
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{9}{4}+{y}^{2}-2y=(y-1)^{2}+\frac{5}{4}≥\frac{5}{4}$;
∴$\overrightarrow{a}•\overrightarrow{b}$的最小值为$\frac{5}{4}$.
故答案为:$\frac{3}{2},\frac{5}{4}$.
点评 考查一个向量在另一个向量方向上的投影的计算公式,向量数乘的运算,向量垂直的充要条件,利用向量坐标解决向量问题的方法,以及向量数量积的坐标运算,配方求二次函数最值的方法.

| A. | 11 | B. | 12 | C. | 20 | D. | 21 |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |
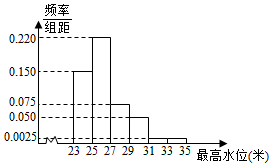 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图: