题目内容
9.已知函数f(x)=xex+c,若方程f(x)=0有两个不相等的实数根,则c的取值范围是(0,$\frac{1}{e}$) .分析 判断f(x)的单调性,计算f(x)的极值和极限,根据零点个数列不等式组解出.
解答 解:f′(x)=ex+xex=ex(1+x),
∴当x<-1时,f′(x)<0,当x>-1时,f′(x)>0,
∴f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,
∴当x=-1时,f(x)取得最小值f(-1)=-$\frac{1}{e}$+c,
∵方程f(x)=0有两个不相等的实数根,
∴f(-1)<0,即-$\frac{1}{e}$+c<0,
∴c<$\frac{1}{e}$.
又x→-∞时,f(x)→c,x→+∞时,f(x)→+∞,
∴c>0,
∴0<e<$\frac{1}{e}$.
故答案为(0,$\frac{1}{e}$).
点评 本题考查了零点个数与函数极值,单调性的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.
该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”的两数之和,表中最后一行仅是一个数,则这个数为( )

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”的两数之和,表中最后一行仅是一个数,则这个数为( )
| A. | 2018×22016 | B. | 2018×22015 | C. | 2017×22016 | D. | 2017×22015 |
17.若$\sqrt{3}$是3a与3b的等比中项,则a+b的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{1}{2}$ |
4.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中百位、十位、个位数字总是从小到大排列的共有( )
| A. | 120个 | B. | 100个 | C. | 300个 | D. | 600个 |
1.已知△ABC的内角A,B,C满足10sinA=12sinB=15sinC,则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{{3\sqrt{15}}}{16}$ | D. | $\frac{5}{48}$ |
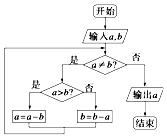 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.