题目内容
1.△ABC中,AB=2,AC=3,∠B=60°,则cosC=( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $±\frac{{\sqrt{6}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 由已知及正弦定理可得sinC=$\frac{ABsinB}{AC}$=$\frac{\sqrt{3}}{3}$,又AB<AC,利用大边对大角可得C为锐角,根据同角三角函数基本关系式即可求得cosC得值.
解答 解:∵AB=2,AC=3,∠B=60°,
∴由正弦定理可得:sinC=$\frac{ABsinB}{AC}$=$\frac{2×\frac{\sqrt{3}}{2}}{3}$=$\frac{\sqrt{3}}{3}$,
又∵AB<AC,C为锐角,
∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{\sqrt{6}}{3}$.
故选:D.
点评 本题主要考查了正弦定理,大边对大角,同角三角函数基本关系式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
16.某企业每天由空气污染造成的经济损失y(单位:元)与空气污染指数API(记为x)的数据统计如下:
(I)求出y与x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(Ⅱ)若该地区某天的空气污染指数为800,预测该企业当天由空气污染造成的经济损失.
附:回归方程中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 空气污染指API(x) | 150 | 200 | 250 | 300 |
| 经济损失y | 200 | 350 | 550 | 800 |
(Ⅱ)若该地区某天的空气污染指数为800,预测该企业当天由空气污染造成的经济损失.
附:回归方程中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
6.已知等差数列{an}的前n项和为Sn,若a1=1,a2=-1,则S4=( )
| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
13.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为( )
| A. | 150 | B. | 180 | C. | 240 | D. | 540 |
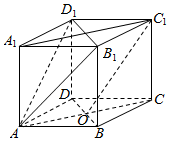 在直平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1=1.
在直平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1=1.