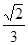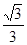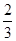题目内容
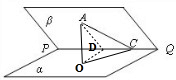
如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ上一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )
| A.1 | B. | C. | D. |
C
解析试题分析:过A作AO⊥α于O,点A到平面α的距离为AO;作AD⊥PQ于D,连接OD,则AD⊥CD,AO⊥OD,∠ADO就是二面角α-PQ-β的大小为60°.∵AC=2,∠ACP=30°,所以AD=ACsin30°=2× =1,在Rt△AOD中,
=1,在Rt△AOD中,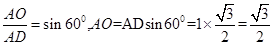 。
。
考点:点、线、面间的距离计算。
点评:本题考查空间几何体中点、线、面的关系,正确作出所求距离是解题的关键,考查计算能力与空间想象能力。

练习册系列答案
相关题目
三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心
的中心 ,则
,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )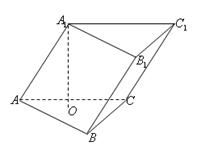
A. | B. |
C. | D. |
设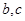 表示两条直线,
表示两条直线,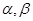 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )
A.若 , ,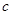 ∥ ∥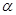 ,则 ,则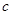 ∥ ∥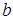 | B.若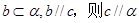 |
C.若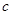 ∥ ∥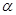 , ,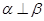 ,则 ,则 | D.若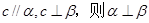 |
若 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )
A.若 ,则 ,则 | B. |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
已知两条不同的直线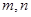 ,两个不同的平面
,两个不同的平面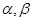 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若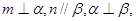 则 则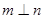 |
B.若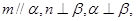 则 则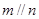 |
C.若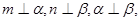 则 则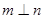 |
D.若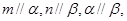 则 则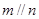 |
在正方体 中,下面结论错误的是( )
中,下面结论错误的是( )
A.BD//平面 | B. |
C. | D.异面直线AD与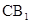 所成角为450 所成角为450 |
如图在棱长均为2的正四棱锥 中,点
中,点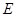 为
为 的中点,则下列命题正确的是( )
的中点,则下列命题正确的是( )
A. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
B. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
C. 不平行面 不平行面 ,且 ,且 与平面 与平面 所成角大于 所成角大于 |
D. 不平行面 不平行面 ,且 ,且 与面 与面 所成角小于 所成角小于 |
如图长方体中,AB=AD=2 ,CC1=
,CC1= ,则二面角C1—BD—C
,则二面角C1—BD—C
的大小为( )
| A.300 | B.450 | C.600 | D.900 |
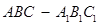 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,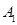 在底面
在底面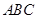 内的射影为
内的射影为
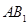 与底面
与底面