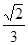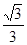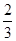题目内容
在空间中,设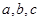 是三条不同的直线,
是三条不同的直线,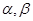 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题:
①若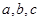 两两相交,则
两两相交,则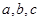 确定一个平面
确定一个平面
②若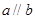 ,且
,且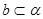 ,则
,则
③若 ,且
,且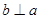 ,则
,则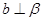
④若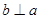 ,且
,且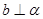 ,则
,则
其中正确的命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:当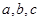 相交于同一点时,则
相交于同一点时,则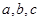 不在同一个平面上,故命题①错误;若
不在同一个平面上,故命题①错误;若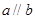 ,且
,且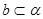 ,则
,则 或
或 ,故命题②错误;根据面面垂直的性质可知命题③正确;若
,故命题②错误;根据面面垂直的性质可知命题③正确;若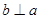 ,且
,且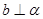 ,则
,则 或
或 ,故命题④错误
,故命题④错误
考点:本题考查了空间中的线面关系
点评:熟练掌握空间中的线面定理是解决空间线面问题判断试题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心
的中心 ,则
,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )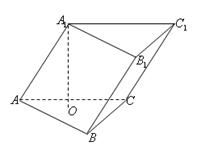
A. | B. |
C. | D. |
设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若m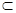 α,n α,n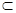 β,m∥n,则α∥β β,m∥n,则α∥β |
| B.若n⊥α,n⊥β,m⊥β,则m⊥α |
| C.若m∥α,n∥β,m⊥n,则α⊥β |
| D.若α⊥β,n⊥β,m⊥n,则m⊥α |
设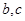 表示两条直线,
表示两条直线,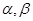 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )
A.若 , ,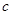 ∥ ∥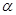 ,则 ,则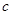 ∥ ∥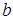 | B.若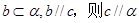 |
C.若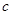 ∥ ∥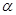 , ,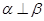 ,则 ,则 | D.若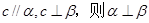 |
如图在棱长均为2的正四棱锥 中,点
中,点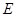 为
为 的中点,则下列命题正确的是( )
的中点,则下列命题正确的是( )
A. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
B. 平行面 平行面 ,且直线 ,且直线 到面 到面 距离为 距离为 |
C. 不平行面 不平行面 ,且 ,且 与平面 与平面 所成角大于 所成角大于 |
D. 不平行面 不平行面 ,且 ,且 与面 与面 所成角小于 所成角小于 |
 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若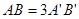 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )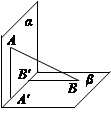
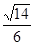
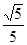
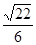
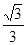
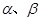 表示两个互相垂直的平面,
表示两个互相垂直的平面,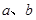 表示一对异面直线,则
表示一对异面直线,则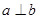 的一个充分条件是( )
的一个充分条件是( )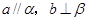 B.
B.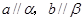
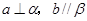 D.
D.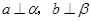
 B.
B.  C.
C. 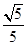 D.
D. 
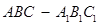 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,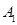 在底面
在底面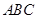 内的射影为
内的射影为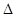
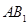 与底面
与底面