题目内容
7.在数列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),则$\frac{a_3}{a_4}$的值是( )| A. | $\frac{15}{16}$ | B. | $\frac{15}{8}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
分析 利用数列递推关系即可得出.
解答 解:a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),
∴a2=1+1=2,2a3=2-1,解得a3=$\frac{1}{2}$.
$\frac{1}{2}{a}_{4}$=$\frac{1}{2}$+1,解得a4=3.
则$\frac{a_3}{a_4}$=$\frac{1}{6}$.
故选:C.
点评 本题考查了数列递推关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.如图的等高条形图可以说明的问题是( )
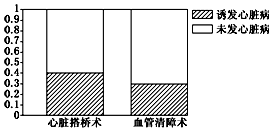

| A. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的 | |
| B. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同 | |
| C. | 此等高条形图看不出两种手术有什么不同的地方 | |
| D. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握 |
2.直线y=-x+b与曲线$y=\sqrt{4-{x^2}}$有且只有两个公共点,则b的取值范围是( )
| A. | 2<b<2$\sqrt{2}$ | B. | 2≤b<2$\sqrt{2}$ | C. | 2≤b≤2$\sqrt{2}$ | D. | 2<b≤2$\sqrt{2}$ |
12.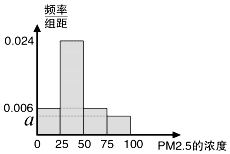 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
(1)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
①求频率分布直方图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(2)将频率视为概率,对于2016年的某3天,记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X,求X的分布列.
 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
①求频率分布直方图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(2)将频率视为概率,对于2016年的某3天,记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X,求X的分布列.
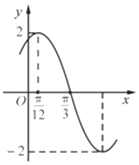 如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象.
如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象.