题目内容
11.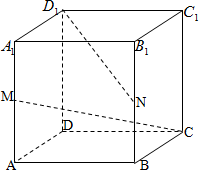 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:(I)异面直线AB与D1N所成的角的正切值;
(II)异面直线CM与D1N所成角的余弦值.
分析 (Ⅰ)由AB∥D1C1,得异面直线CM与D1N所成角为∠C1D1N,由此能求出异面直线AB与D1N所成的角的正切值.
(Ⅱ)推导出四边形BND1E是平行四边形,从而D1N∥BE,进而∠BOC=θ是异面直线CM与D1N所成角,由此能求出异面直线CM与D1N所成角的余弦值.
解答 解:(Ⅰ)∵正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.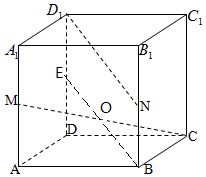
∴AB∥D1C1,
∴异面直线CM与D1N所成角为∠C1D1N,
设正方体ABCD-A1B1C1D1中棱长为2,则C1N=$\sqrt{5}$,
∴tan∠C1D1N=$\frac{{{C_1}N}}{{{C_1}{D_1}}}=\frac{{\sqrt{5}}}{2}$,
∴异面直线AB与D1N所成的角的正切值为$\frac{\sqrt{5}}{2}$.
(Ⅱ)不妨设正方体棱长为2,取DD1的中点E,连结BE,
由题意知ME∥BC,∴CM与BE相交于O点,
∵D1E$\underset{∥}{=}$BN,∴四边形BND1E是平行四边形,
∴D1N∥BE,∴∠BOC=θ是异面直线CM与D1N所成角,
∵OB=OC=$\frac{1}{2}$MC=$\frac{1}{2}$$\sqrt{1+{{(2\sqrt{2})}^2}}=\frac{3}{2}$,
∴$cosθ=\frac{{\frac{9}{4}+\frac{9}{4}-4}}{{2×\frac{9}{4}}}=\frac{1}{9}$,
∴异面直线CM与D1N所成角的余弦值为$\frac{1}{9}$.
点评 本题考查异面直线所成角的正切值和余弦值的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力、数据处理能力,考查函数与方程思想、化归与转化思想、数形结合,考查创新意识、应用意识,是中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | 2<b<2$\sqrt{2}$ | B. | 2≤b<2$\sqrt{2}$ | C. | 2≤b≤2$\sqrt{2}$ | D. | 2<b≤2$\sqrt{2}$ |
| A. | 由样本数据得到的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小说明拟合效果越好 | |
| D. | 若变量y和x之间的相关系数为r=-0.9462,则变量y和x之间具有线性相关关系 |
| A. | x=-1 | B. | $x=-\frac{1}{2}$ | C. | x=1 | D. | $x=\frac{3}{2}$ |