题目内容
14.判断集合A与B是否相等?(1)A={0},B=∅;
(2)A={…,-5,-3,-1,1,3,5,…},B={x|x=2m+1,m∈Z};
(3)A={x|x=2m-1,m∈N},B={x|x=2m+1,m∈N}.
分析 分析集合中的元素,即可得出结论.
解答 解:(1)A={0}表示集合中有元素0,B=∅表示集合中没有元素,所以A≠B;
(2)A={…,-5,-3,-1,1,3,5,…}表示奇数集,B={x|x=2m+1,m∈Z},表示奇数集,所以A=B;
(3)A={x|x=2m-1,m∈N}比B={x|x=2m+1,m∈N}多一个元素-1,所以A≠B.
点评 本题考查集合的相等,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
4.用随机数表法从100名学生(男生20人)中抽选25人进行评教,某男学生被抽到的可能性是( )
| A. | 0.01 | B. | 0.04 | C. | 0.2 | D. | 0.25 |
5.运行如图的程序,若输入的数为1,则输出的数是( )


| A. | -2 | B. | 0 | C. | 1 | D. | 3 |
9.已知点A(cos80°,sin80°),B(cos20°,sin20°),则|$\overrightarrow{AB}$|等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
3.已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a2=3,那么a12等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
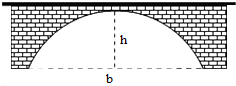 如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.
如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.