题目内容
7.已知抛物线的顶点在原点,对称轴是x轴,直线y=2x-4截抛物线弦长|AB|=$3\sqrt{5}$,求抛物线标准方程及它的准线方程.分析 设抛物线方程为y2=2px(p≠0),将直线方程y=2x-4代入,并整理,利用韦达定理,结合弦长公式,即可求抛物线的方程及它的准线方程.
解答 解:设所求的抛物线方程为 y2=ax (a≠0),A((x1,y1),B(x2,y2)
由y2=ax与y=2x-4,消去y得4x2-( a+16)x+16=0 …(2分)
由△=(a+16)2-256>0得a>0,或a<-32
∵x1+x2=$\frac{a+16}{4}$x1 x2=4 …(4分)
∴|AB|=$\sqrt{(1+{2^2})[{{({x_1}+{x_2})}^2}-4{x_1}•{x_2}]}$=$\sqrt{5[{{(\frac{a+16}{4})}^2}-16]}$
∴$\sqrt{5[{{(\frac{a+16}{4})}^2}-16]}$=45
∴a=4或a=-36 …(8分)
∴所求抛物线方程为y2=4x或y2=-36x …(10分)
准线方程分别为x=-1,x=9 …(12分)
点评 本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查抛物线的弦长计算,属于中档题.

练习册系列答案
相关题目
3.已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a2=3,那么a12等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
2.抛物线4y=x2的焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
19.若cos($\frac{π}{6}-x$)=-$\frac{1}{3}$,则cos($2x+\frac{2π}{3}$)=( )
| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
17.与二进制数110(2)相等的十进制数是( )
| A. | 6 | B. | 7 | C. | 10 | D. | 11 |
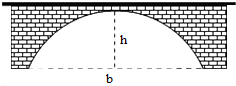 如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.
如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.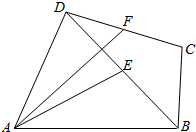 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.