题目内容
8.已知函数f(x)=ex-e-x,e为自然对数的底,则下列结论正确的是( )| A. | f(x)为奇函数,且在R上单调递增 | B. | f(x)为偶函数,且在R上单调递增 | ||
| C. | f(x)为奇函数,且在R上单调递减 | D. | f(x)为偶函数,且在R上单调递减 |
分析 可先得出f(x)的定义域为R,求f(-x)=-f(x),从而得出f(x)为奇函数,根据指数函数的单调性便可看出x增大时,f(x)增大,从而得到f(x)在R上单调递增,这样便可找出正确选项.
解答 解:f(x)的定义域为R;
f(-x)=e-x-ex=-f(x);
∴f(x)为奇函数;
x增加时,e-x减小,-e-x增加,且ex增加,∴f(x)增加;
∴f(x)在R上单调递增.
故选A.
点评 考查奇函数的定义,判断一个函数为奇函数的方法和过程,以及增函数的定义,指数函数的单调性.

练习册系列答案
相关题目
19.若cos($\frac{π}{6}-x$)=-$\frac{1}{3}$,则cos($2x+\frac{2π}{3}$)=( )
| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
3.已知a=log32,b=log2$\frac{1}{3}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
13.某种型号的电脑自投放市场以来,经过三次降价,单价由原来的5000元降到2560元,则平均每次降价的百分率是( )
| A. | 10% | B. | 15% | C. | 16% | D. | 20% |
17.与二进制数110(2)相等的十进制数是( )
| A. | 6 | B. | 7 | C. | 10 | D. | 11 |
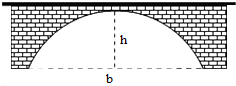 如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.
如图,一桥拱的形状为抛物线,此时水面距桥拱顶端h=6m,水面宽b=24m,若水面上升2m后,水面宽为8$\sqrt{6}$米.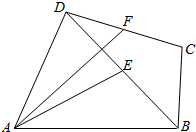 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.