题目内容
(本小题满分14分)直棱柱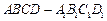 中,底面
中,底面 是直角梯形,
是直角梯形,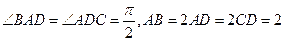
(Ⅰ)求证: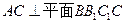
(Ⅱ)在 上是否存一点
上是否存一点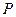 ,使得
,使得 与平面
与平面
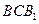 与平面
与平面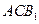 都平行?证明你的结论.
都平行?证明你的结论.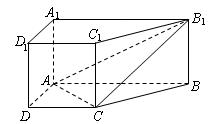
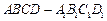 中,底面
中,底面 是直角梯形,
是直角梯形,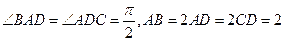
(Ⅰ)求证:
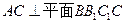
(Ⅱ)在
 上是否存一点
上是否存一点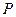 ,使得
,使得 与平面
与平面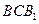 与平面
与平面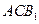 都平行?证明你的结论.
都平行?证明你的结论.
证明:(Ⅰ) 直棱柱
直棱柱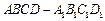 中,
中,
 BB1⊥平面ABCD,
BB1⊥平面ABCD,
 BB1⊥AC.…2分
BB1⊥AC.…2分
又 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,
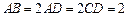 ,
,
∴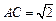 ,∠CAB=45°,
,∠CAB=45°,
∴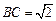 ,
,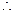 BC⊥AC. ……5分
BC⊥AC. ……5分
又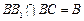 ,
, 平面B
平面B B1C1C,
B1C1C,
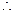 AC⊥平面BB1C1C…7分
AC⊥平面BB1C1C…7分
(Ⅱ)在 上是否存一点
上是否存一点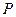 ,使得
,使得 与平面
与平面
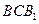 与平面
与平面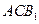 都平行?证明你的结论.
都平行?证明你的结论.
解:存在点P,P为A1B1的中点. ………………………8分
证明:由P为A1B1的中点,
有PB1‖AB,且PB1=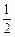 AB.…………9分
AB.…………9分
又∵DC‖AB,DC=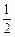 AB,
AB,
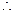 DC∥PB1,且DC= PB1,
DC∥PB1,且DC= PB1,
∴DCB1P为平行四边形,
从而CB1∥DP. …………… ……11分
又CB1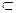 面ACB1,DP
面ACB1,DP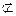 面ACB1,
面ACB1,
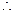 DP∥面ACB1. …………12分
DP∥面ACB1. …………12分
同理, ∥面BCB1. ……………………………………13分
∥面BCB1. ……………………………………13分
故P为A1B1的中点符合题意…………………………14分
 直棱柱
直棱柱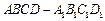 中,
中, BB1⊥平面ABCD,
BB1⊥平面ABCD,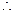 BB1⊥AC.…2分
BB1⊥AC.…2分又
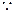 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,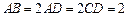 ,
,∴
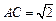 ,∠CAB=45°,
,∠CAB=45°,∴
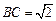 ,
,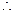 BC⊥AC. ……5分
BC⊥AC. ……5分又
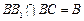 ,
, 平面B
平面B B1C1C,
B1C1C,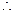 AC⊥平面BB1C1C…7分
AC⊥平面BB1C1C…7分(Ⅱ)在
 上是否存一点
上是否存一点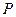 ,使得
,使得 与平面
与平面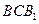 与平面
与平面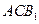 都平行?证明你的结论.
都平行?证明你的结论.解:存在点P,P为A1B1的中点. ………………………8分
证明:由P为A1B1的中点,
有PB1‖AB,且PB1=
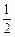 AB.…………9分
AB.…………9分又∵DC‖AB,DC=
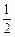 AB,
AB,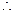 DC∥PB1,且DC= PB1,
DC∥PB1,且DC= PB1,∴DCB1P为平行四边形,
从而CB1∥DP. …………… ……11分
又CB1
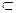 面ACB1,DP
面ACB1,DP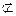 面ACB1,
面ACB1,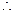 DP∥面ACB1. …………12分
DP∥面ACB1. …………12分同理,
 ∥面BCB1. ……………………………………13分
∥面BCB1. ……………………………………13分故P为A1B1的中点符合题意…………………………14分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.
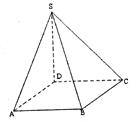
 SC; (II)求平
SC; (II)求平 面SBC与平面ABCD所成二面角的大小;
面SBC与平面ABCD所成二面角的大小;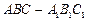 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是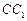 的中点,直线
的中点,直线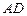 与侧面
与侧面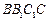 所成的角是
所成的角是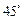 .
.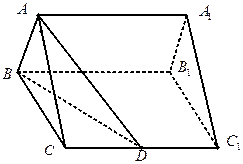
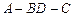 的大小;
的大小;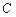 到平面
到平面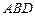 的距离.
的距离.  求证:EF⊥平面PCD。
求证:EF⊥平面PCD。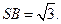
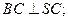
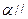 平面
平面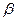 ,
,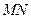 和
和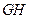 是夹在
是夹在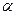 、
、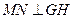 ,
,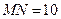 直线
直线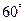 角,则线段
角,则线段 B.
B. C.
C. D.
D.