题目内容
、如图，四棱锥S—ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SD=1,SB=
.
（I）求证BC
SC； （II）求平
面SBC与平面ABCD所成二面角的大小；
（III）设棱SA的中点为M，求异面直线DM与SB所成角的大小
.（I）求证BC
SC； （II）求平面SBC与平面ABCD所成二面角的大小；（III）设棱SA的中点为M，求异面直线DM与SB所成角的大小
（I）∵底面ABCD是正方形， ∴BC⊥DC
∵SD⊥底面ABCD，∴SD⊥BC，又DC∩SD=D，
∴BC⊥平面SDC ∴BC⊥SC.….4分
（II）∵平面SBC∩平面ABCD＝BC ，由（I）知SC⊥BC，又CD⊥BC
∴∠SCD为所求二面角的平面角,……6分 ∵SD="DC=1," ∴∠SCD=45°…8分
（III）
取AB中点P，连结MP，DP.
在△ABS中，由中位线定理得 MP//SB，
是异面直线DM与SB所成的角….10分
，又
∴在△DMP中，有DP2=MP2+DM2
， 
…12分
∵SD⊥底面ABCD，∴SD⊥BC，又DC∩SD=D，
∴BC⊥平面SDC ∴BC⊥SC.….4分（II）∵平面SBC∩平面ABCD＝BC ，由（I）知SC⊥BC，又CD⊥BC
∴∠SCD为所求二面角的平面角,……6分 ∵SD="DC=1," ∴∠SCD=45°…8分
（III）
取AB中点P，连结MP，DP.在△ABS中，由中位线定理得 MP//SB，
是异面直线DM与SB所成的角….10分，又∴在△DMP中，有DP2=MP2+DM2
， …12分略
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
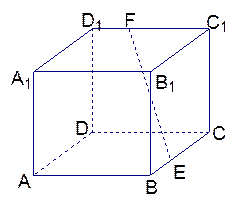
中，底面
是直角梯形，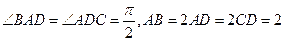
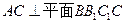
上是否存一点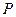
，使得
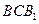与平面
与平面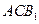
都平行？证明你的结论．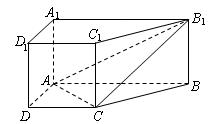
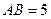，AA1＝3，点D是AB的中点．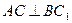
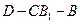的大小．
，
，
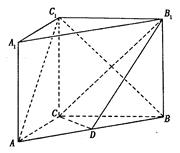
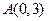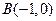，求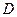
点的坐标，使四边形
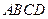为直角梯形．
本题满分10分）
求证：a∥l.