题目内容
12．设i是虚数单位，复数z满足（1+i）z=2i50，则z的共轭复数$\overline{z}$为（ ）| A． | 1+i | B． | 1-i | C． | -1+i | D． | -1-i |
分析 根据条件先化简复数，求出z，然后根据共轭复数的定义进行求解即可．
解答 解：∵（1+i）z=2i50=-2，
∴z=$\frac{-2}{1+i}$=$\frac{-2（1-i）}{2}$=-1+i，
则$\overline{z}$=-1-i，
故选：D
点评 本题主要考查共轭复数的求解，根据复数的基本运算先求出z是解决本题的关键．比较基础．
练习册系列答案
口算题天天练系列答案
相关题目
7．已知双曲线E的渐近线方程为3x±4y=0，且E的右焦点为（5，0），过双曲线E中心的直线与双曲线E交于A，B两点，在双曲线E上取一点C，直线AC，BC的斜率分别为k1、k2，则k1k2等于（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{9}{16}$ | D． | $\frac{16}{25}$ |
17．今年春节期间，在为期5天的某民俗庙会上，某摊点销售一种儿童玩具的情况如表：
由表可知：两个雨天的平均销售量为100件/天，三个非雨天的平均销售量为125件/天．
（1）以十位位数字为茎，个位数字为叶．画出表中10个销售数据的茎叶图，并求出这组数据的中位数
（2）假如明年庙会5天中每天下雨的概率为$\frac{2}{5}$，且每天下雨与否相互独立，其它条件不变．试估计庙会期间同一类型摊点能够售出的同种儿童玩具的件数；
（3）已知摊位租金为1000元/个，该种玩具进货价为9元/件，售价为13元/件，未售出玩具可按进货价退回厂家，若所获利润大于1200元的概率超过0.6，则成为“值得投资”，那么在（2）的条件下，你认为“值得投资”吗？
| 日期 | 2月13日 | 2月14日 | 2月15日 | 2月16日 | 2月17日 | |
| 天气 | 小雨 | 小雨 | 阴 | 阴转多云 | 多云转阴 | |
| 销售量 | 上午 | 42 | 47 | 58 | 60 | 63 |
| 下午 | 55 | 56 | 62 | 65 | 67 | |
（1）以十位位数字为茎，个位数字为叶．画出表中10个销售数据的茎叶图，并求出这组数据的中位数
（2）假如明年庙会5天中每天下雨的概率为$\frac{2}{5}$，且每天下雨与否相互独立，其它条件不变．试估计庙会期间同一类型摊点能够售出的同种儿童玩具的件数；
（3）已知摊位租金为1000元/个，该种玩具进货价为9元/件，售价为13元/件，未售出玩具可按进货价退回厂家，若所获利润大于1200元的概率超过0.6，则成为“值得投资”，那么在（2）的条件下，你认为“值得投资”吗？
1．若数列{an}满足a1=1，a2=$\frac{2}{3}$，2an-1an+1=anan+1+an-1an（n≥2），则an=（ ）
| A． | $\frac{2}{n+1}$ | B． | $\frac{2}{n+2}$ | C． | （$\frac{2}{3}$）n | D． | （$\frac{2}{3}$）n-1 |
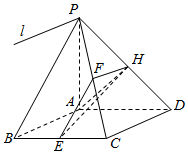如图，已知四棱锥P-ABCD的底面是菱形，PA⊥平面ABCD，∠ABC=60°，E，F，H分别是BC，PC，PD的中点．