题目内容
2.已知数列{an}是公差为整数的等差数列,前n项和为Sn,且a1+a5+2=0,2S1,3S2,8S3成等比数列,则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前10项和为-$\frac{10}{51}$.分析 根据a1+a5+2=0,求出a3=-1,2S1,3S2,8S3成等比数列,求得d=-2,$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{2}(\frac{1}{2n-5}-\frac{1}{2n-3})$,再求和.
解答 解:数列{an}是公差为整数的等差数列,首项为a1,公差为d,
a1+a5+2=0,a1+a1+4d+2=0,
∴a3=-1,
2S1,3S2,8S3成等比数列,
∴9${S}_{2}^{2}$=2S1×8S3,
∴9$({a}_{1}+{a}_{2})^{2}$=2a1×8(a1+a2+a3),
9$({2a}_{3}-3d)^{2}$=2(a3-2d)×8(3a3-3d),
将a3=-1代入,整理得:5d2+12d+4=0,
解得:d=-2或d=$-\frac{2}{5}$(舍去),
∴an=-2n+5,
(2)an•an+1=(-2n+5)(-2n+3),
$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-5)(2n-3)}$=$\frac{1}{2}(\frac{1}{2n-5}-\frac{1}{2n-3})$;
∴T10=b1+b2+b3+…+b10,
=$\frac{1}{2}$×{[$-\frac{1}{3}$-(-1)]+(-1-1)+(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{15}$-$\frac{1}{17}$)}
=-$\frac{10}{51}$.
故答案为:-$\frac{10}{51}$.
点评 本题考查求数列的通项及前n项和,过程比较繁琐,属于中档题.

练习册系列答案
相关题目
10.已知a<b<0,c∈R,下列不等式恒成立的是( )
| A. | ac<bc | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a-b}$$>\frac{1}{a}$ | D. | a2<b2 |
17.已知函数f(x)为偶函数,且当x≤0时,f(x)=$\frac{10+3x+{2}^{-x}}{7}$+|$\frac{10+3x-{2}^{-x}}{7}$|+m,若函数f(x)有4个零点,则实数m的取值范围为( )
| A. | (-$\frac{20}{7}$,-$\frac{8}{7}$) | B. | (-∞,-3)∪(-$\frac{8}{7}$,+∞) | C. | (-2,-$\frac{10}{7}$) | D. | (-∞,-2)∪(-$\frac{10}{7}$,+∞) |
7.已知F1、F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点.过F2作双曲线的渐近线的垂线,垂足为P,则|PF1|2-|PF2|2=( )
| A. | 4a2 | B. | 4b2 | C. | 3a2+b2 | D. | a2+3b2 |
12.设i是虚数单位,复数z满足(1+i)z=2i50,则z的共轭复数$\overline{z}$为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
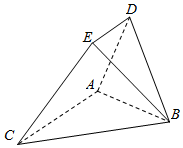 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.