题目内容
4.已知等差数列{an}的前n项和为Sn,S11=22,a4=-12,如果当n=m时,Sn最小,那么m的值为( )| A. | 10 | B. | 9 | C. | 5 | D. | 4 |
分析 设等差数列{an}的公差为d,由于S11=22,a4=-12,可得:11a1+$\frac{11×10}{2}$d=22,a1+3d=-12,解出可得:a1,d.由an≤0,解出即可得出.
解答 解:设等差数列{an}的公差为d,∵S11=22,a4=-12,
∴11a1+$\frac{11×10}{2}$d=22,a1+3d=-12,
解得a1=-33,d=7.
∴an=-33+7(n-1)=7n-40,
由an≤0,解得n≤$\frac{40}{7}$.
∴当n=5时,Sn最小,
故选:C.
点评 本题考查了等差数列的通项公式及其前n项和公式、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
12.设i是虚数单位,复数z满足(1+i)z=2i50,则z的共轭复数$\overline{z}$为( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
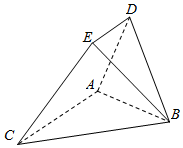 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.