题目内容
若x>4,则函数y=x+
( )
| 1 |
| x-4 |
| A、有最大值-6 |
| B、有最小值6 |
| C、有最大值-2 |
| D、有最小值2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:先将原函数变换为y=x-4+
+4,然后令t=x-4(t>0),则原函数可化为求函数y=t+
+4(t>0)的最值问题,然后利用导数或基本不等式都很容易求解.
| 1 |
| x-4 |
| 1 |
| t |
解答:
解:原函数可化为y=x-4+
+4,令t=x-4(t>0),
则原函数可化为求函数y=t+
+4(t>0),
所以y′=1-
,令y′≥0得t≥1;令y′<0得0<t<1,
所以函数y=t+
+4(t>0)在区间(0,1)上递减,在[1,+∞)上递增,
且当x→0或x→+∞时,y都趋向于正无穷大,
当t=1是,函数取得最小值6,无最大值.
故答案选:B
方法二:y=x-4+
+4≥2+4=6
| 1 |
| x-4 |
则原函数可化为求函数y=t+
| 1 |
| t |
所以y′=1-
| 1 |
| t2 |
所以函数y=t+
| 1 |
| t |
且当x→0或x→+∞时,y都趋向于正无穷大,
当t=1是,函数取得最小值6,无最大值.
故答案选:B
方法二:y=x-4+
| 1 |
| x-4 |
点评:关于函数的最值问题一般考虑其单调性,而单调性常用导数来研究,此例先换元,使函数变得简单了后再求解.当然此题也可以利用基本不等式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数幂函数有( )个.
y=2x2;y=x2;y=x2+x;y=
.
y=2x2;y=x2;y=x2+x;y=
| 1 |
| x2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数中,周期为π的函数是( )
A、y=sin
| ||
| B、y=|sinx| | ||
| C、y=sinx+|sinx| | ||
D、y=|sinx+
|
在三角形ABC中,AB=3,AC=4,BC=
,则AC边上的高为( )
| 13 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
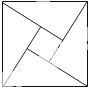 2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
幂函数y=xm与y=xn在第一象限内的图象如图所示,则( )


| A、-1<n<0,<m<1 |
| B、n<-1,0<m<1 |
| C、-1<n<0,m>1 |
| D、n<-1,m>1 |
设(x,y)在映射f下的象是(x+y,x-y),则象(1,2)的原象是( )
| A、(3,1) | ||||
B、(
| ||||
| C、(-1,3) | ||||
D、(-
|
某人向一个边长为2的正方形盘面上均匀地撒了400粒大米,其中落在该正方形的内切圆里有314粒,据此可估计圆周率π的值约为( )
| A、2 | B、3 | C、3.14 | D、4 |