题目内容
17.各项均为正数的数列{an}和{bn}满足:an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,且a1=1,a2=3,则数列{an}的通项公式为${a_n}=\frac{{{n^2}+n}}{2}$.分析 利用等差数列和等比数列中项的性质,运用等差数列的定义证明数列{$\sqrt{{b}_{n}}$}是等差数列.再利用等差数列的通项公式求出$\sqrt{{b}_{n}}$的通项公式,进而求出bn,an.
解答 解:∵an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,
∴2bn=an+an+1①,
an+12=bn•bn+1②.
由②得an+1=$\sqrt{{b}_{n}{b}_{n+1}}$③.
将③代入①得,对任意n≥2,n∈N*,
有2bn=$\sqrt{{b}_{n-1}{b}_{n}}$+$\sqrt{{b}_{n}{b}_{n+1}}$.
∵bn>0,
∴2$\sqrt{{b}_{n}}$=$\sqrt{{b}_{n-1}}$+$\sqrt{{b}_{n+1}}$,
∴{$\sqrt{{b}_{n}}$}是等差数列.
设数列{$\sqrt{{b}_{n}}$}的公差为d,
由a1=1,b1=2,a2=3,得b2=$\frac{9}{2}$.
∴$\sqrt{{b}_{1}}$=$\sqrt{2}$,$\sqrt{{b}_{2}}$=$\frac{3\sqrt{2}}{2}$,
d=$\sqrt{{b}_{2}}$-$\sqrt{{b}_{1}}$=$\frac{\sqrt{2}}{2}$.
∴$\sqrt{{b}_{n}}$=$\sqrt{2}$+$\frac{\sqrt{2}}{2}$(n-1)=$\frac{\sqrt{2}}{2}$(n+1),
∴bn=$\frac{1}{2}$(n+1)2,
an=$\sqrt{{b}_{n-1}{b}_{n}}$=$\frac{1}{2}$n(n+1)=$\frac{{n}^{2}+n}{2}$.
故答案为:${a_n}=\frac{{{n^2}+n}}{2}$.
点评 本题考查了等差、等比数列的通项公式,利用构造等差数列法求得数列{$\sqrt{{b}_{n}}$}的通项公式是解答本题的突破口,本题还考查了学生的运算能力,运算要细心.

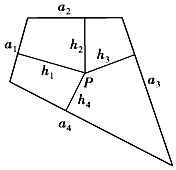 如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )
如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{3V}{K}$ | D. | $\frac{V}{3K}$ |
| A. | [0,+∞) | B. | [1,3] | C. | (-1,-$\frac{1}{3}$] | D. | [-1,-$\frac{1}{3}$] |