题目内容
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G、F分别是线段CE、PB的中点.

(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求二面角 的正切值.
的正切值.

(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求二面角
 的正切值.
的正切值.(Ⅰ)详见解析;(Ⅱ)二面角 的正切值为
的正切值为 .
.
 的正切值为
的正切值为 .
.试题分析:(Ⅰ)连结BD,因为E是AD的中点
 是CE的中点,所以BD过
是CE的中点,所以BD过 点,这样只需证
点,这样只需证 即可;(Ⅱ)求二面角
即可;(Ⅱ)求二面角 的正切值,需找出平面角,注意到PA⊥平面ABCD,F是线段PB的中点,取
的正切值,需找出平面角,注意到PA⊥平面ABCD,F是线段PB的中点,取 的中点
的中点 ,则
,则 ⊥平面ABCD,过
⊥平面ABCD,过 作
作 ,垂足为
,垂足为 ,则
,则 即为二面角
即为二面角 的平面角.
的平面角.试题解析:(Ⅰ)证明:连结
 ,因为E是AD的中点,
,因为E是AD的中点, 是CE的中点,且ABCE为菱形,
是CE的中点,且ABCE为菱形, ,
, ,所以
,所以 过
过 点,且
点,且 是
是 的中点,在
的中点,在 中,又因为
中,又因为 是
是 的中点,
的中点, ,又
,又 平面
平面 ,
, 平面
平面 ;
;(Ⅱ)取
 的中点
的中点 ,因为
,因为 是
是 的中点,
的中点, ,又因为
,又因为 平面
平面 ,
, 平面
平面 ,过
,过 作
作 ,垂足为
,垂足为 ,连结
,连结 ,则
,则 即为二面角
即为二面角 的平面角,
的平面角,不妨令
 ,则
,则 ,有平面几何知识可知
,有平面几何知识可知 ,
, ,所以二面角
,所以二面角 的正切值为
的正切值为 .
.

练习册系列答案
相关题目
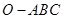 的侧棱
的侧棱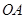 、
、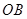 、
、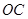 两两垂直,且
两两垂直,且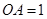 ,
,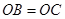
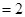 ,
,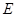 是
是
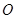 点到面
点到面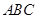 的距离;
的距离;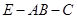 的正弦值.
的正弦值.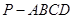 的底面为平行四边形,
的底面为平行四边形,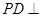 平面
平面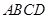 ,
,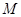 为
为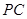 中点.
中点.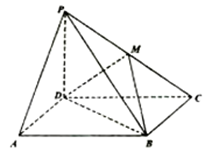
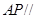 平面
平面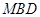 ;
;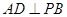 ,求证:
,求证: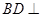 平面
平面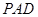 .
.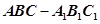 中,AB=BC,
中,AB=BC,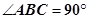 ,Q是AC上的点,AB1//平面BC1Q.
,Q是AC上的点,AB1//平面BC1Q.
 ,求二面角Q-BC1—C的余弦值.
,求二面角Q-BC1—C的余弦值.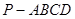 中,
中,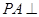 底面
底面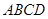 ,面
,面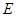 为侧棱
为侧棱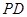 上一点,
上一点,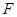 为
为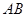 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.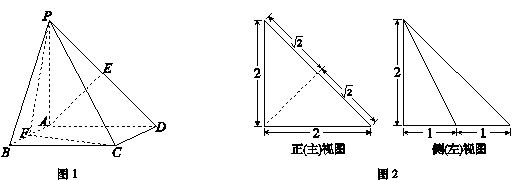
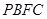 的体积;
的体积;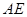 ∥平面
∥平面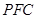 ;
;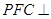 平面
平面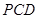 .
.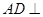 平面
平面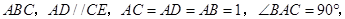 凸多面体
凸多面体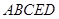 的体积为
的体积为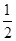 ,
,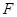 为
为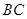 的中点.
的中点.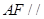 平面
平面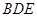 ;
;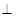 平面
平面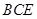 .
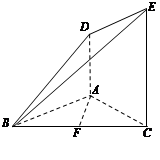
. 
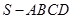 的底面边长为
的底面边长为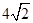 ,高
,高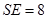 ,则过点
,则过点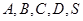 的球的半径为( )
的球的半径为( )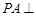 ⊙
⊙ 所在的平面,
所在的平面, 是⊙
是⊙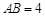 ,C是⊙
,C是⊙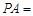
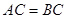 ,
,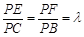 .
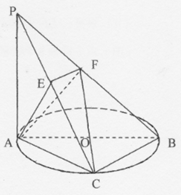
.
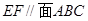 ;
;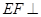
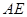 ;
;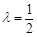 时,求三棱锥
时,求三棱锥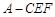 的体积.
的体积.