题目内容
13.已知函数f(x)=log2(x+1),g(x)=ex(Ⅰ)若F(x)=f(2x)+kx为偶函数,求k的值;
(Ⅱ)判断h(x)=f(x)+g(x)在其定义域上的单调性,若h(x)具有单调性,请用定义证明;若不具有单调性,请说明理由.
分析 (Ⅰ)根据函数奇偶性的定义得到2k+1=0,求出k的值即可;(Ⅱ)根据函数单调性的定义判断即可.
解答 解:(Ⅰ)∵函数F(x)=log2(2x+1)+kx(k为常数)是偶函数,
∴f(-x)=f(x),即 log2( 2-x+1)-kx=log2( 2x+1)+kx,
即log2( 2x+1)-x-kx=log2( 2x+1)+kx,可得(2k+1)x=0,
∴2k+1=0,∴k=-$\frac{1}{2}$;
(Ⅱ)∵f(x)=log2(x+1),g(x)=ex在(-1,+∞)递增,
∴h(x)=f(x)+g(x)在其定义域上单调递增,
不妨设-1<x1<x2,
则h(x1)-h(x2)=log2(x1+1)+${e}^{{x}_{1}}$-log2(x2+1)-${e}^{{x}_{2}}$,
=log2$\frac{{x}_{1}+1}{{x}_{2}+1}$+(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)
∵x1<x2,
∴$\frac{{x}_{1}+1}{{x}_{2}+1}$<1,${e}^{{x}_{1}}$-${e}^{{x}_{2}}$<0,
故h(x1)-h(x2)<0,
故h(x)在(-1,+∞)递增.
点评 本题考查了函数的单调性和奇偶性问题,考查对数函数以及指数函数的性质,是一道中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
1.定义区间[x1,x2]的长度为x2-x1(x2>x1)单调递增),函数$f(x)=\frac{{({a^2}+a)x-1}}{{{a^2}x}}$(a∈R,a≠0)的定义域与值域都是[m,n](n>m),则区间[m,n]取最大长度时实数a的值( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
18.设α,β是两个平面,直线a?α则“a∥β”是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.在底面是菱形的四棱锥P-ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则$\frac{AK}{PK}$等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
20.执行如图所示的程序框图,输出的S=( )
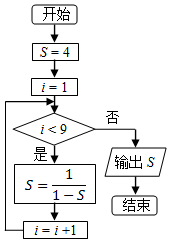

| A. | 4 | B. | $-\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
 中,
中, ,则
,则 .
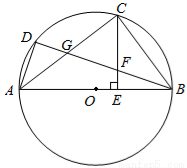
.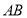 为圆
为圆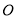 的直径,
的直径,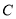 ,
,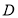 是圆
是圆 上的两个点,
上的两个点,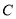 是劣弧
是劣弧 的中点,
的中点,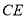 ⊥
⊥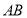 于
于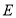 ,
,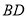 交
交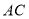 于
于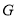 ,交
,交 于
于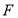 .
.
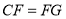 ;
;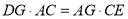 .
.