题目内容
8.($\sqrt{x}$-$\frac{1}{x}$)5的二项展开式中,含x的一次项的系数为-5(用数字作答).分析 写出二项展开式的通项,由x的指数等于1求得r值,则答案可求.
解答 解:($\sqrt{x}$-$\frac{1}{x}$)5的二项展开式中,通项公式为:
Tr+1=${C}_{5}^{r}$•${(\sqrt{x})}^{5-r}$•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{5}^{r}$•${x}^{\frac{5-3r}{2}}$,
令$\frac{5-3r}{2}$=1,得r=1;
∴二项式($\sqrt{x}$-$\frac{1}{x}$)5的展开式中含x的一次项系数为:
-1•${C}_{5}^{1}$=-5.
故答案为:-5.
点评 本题考查了二项式系数的性质与应用问题,关键是对二项展开式通项的记忆与应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知A(-m,0),B(m,0)(m>2)若三角形ABC内切圆的圆心在直线x=1上运动,则顶点C轨迹方程可能为( )
| A. | ${x^2}-\frac{y^2}{6}=1$ | B. | ${x^2}-\frac{y^2}{6}=1(x>1)$ | C. | $\frac{x^2}{4}-\frac{y^2}{8}=1(x>2)$ | D. | $\frac{x^2}{4}-\frac{y^2}{8}=1$ |
14.若函数f(x)=a(x-2)ex+lnx+$\frac{1}{x}$在(0,2)上存在两个极值点,则a的取值范围为( )
| A. | (-∞,-$\frac{1}{4{e}^{2}}$) | B. | (-$\frac{1}{e}$,$\frac{1}{4{e}^{2}}$)∪(1,+∞) | ||
| C. | (-∞,-$\frac{1}{e}$) | D. | (-∞,-$\frac{1}{e}$)∪(--$\frac{1}{e}$,-$\frac{1}{4{e}^{2}}$) |
15.i是虚数单位,(1-i)Z=2i,则复数Z的模|Z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 中,角
中,角 所对的边分别为
所对的边分别为 ,满足
,满足 .
. ;
; 的取值范围.
的取值范围.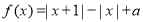 .
.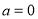 ,求不等式
,求不等式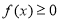 的解集;
的解集;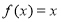 有三个不同的解,求
有三个不同的解,求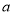 的取值范围.
的取值范围.