题目内容
8．已知i为虚数单位，若复数z满足|z-3-4i|=1，求|z|的最大值．分析 由题意画出图形，然后由复数模的几何意义求得|z|的最大值．
解答 解：由复数模的几何意义可知
满足|z-3-4i|=1的复数z在复平面内对应的点的轨迹是以（3，4）为圆心，以1为半径的圆，
如图，
∵圆心（3，4）到原点O的距离为$\sqrt{{3}^{2}{+4}^{2}}$=5，
∴|z|的最大值为5+1=6．
故选：D．
点评 本题考查复数的代数表示法及其几何意义，考查了复数的模，是基础题．
练习册系列答案
口算能手系列答案
相关题目
18．设函数f（x）在点x0附近有定义，且有f（x0+△x）-f（x0）=a△x+b（△x）2，其中a，b为常数，则（ ）
| A． | f'（x）=a | B． | f'（x）=b | C． | f'（x0）=a | D． | f'（x0）=b |
16．已知正三棱柱ABC-A1B1C1的六个顶点在球O1上，又知球O2与此正三棱柱的5个面都相切，求球O1与球O2的表面积之比（ ）
| A． | 5：1 | B． | 2：1 | C． | 4：1 | D． | $\sqrt{3}$：1 |
13．已知函数f（x）=$\sqrt{2}$sinωx-$\sqrt{2}$cosωx（ω＜0），若y=f（x+$\frac{π}{4}$）的图象与y=f（x-$\frac{π}{4}$）的图象重合，记ω的最大值为ω0，函数g（x）=cos（ω0x-$\frac{π}{3}$）的单调递增区间为（ ）
| A． | [-$\frac{1}{3}$π+$\frac{kπ}{2}$，-$\frac{π}{12}$+$\frac{kπ}{2}$]（k∈Z） | B． | [-$\frac{π}{12}$+$\frac{kπ}{2}$，$\frac{π}{6}$+$\frac{kπ}{2}$]（k∈Z） | ||
| C． | [-$\frac{1}{3}$π+2kπ，-$\frac{π}{12}$+2kπ]（k∈Z） | D． | [-$\frac{π}{12}$+2kπ，-$\frac{π}{6}$+2kπ]（k∈Z） |
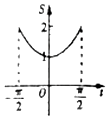
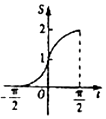
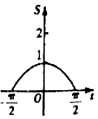
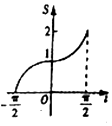
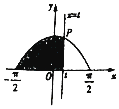在函数y=cosx，$x∈[{-\frac{π}{2}，\frac{π}{2}}]$的图象上有一点P（t，cost），若该函数的图象与x轴、直线$x=-\frac{π}{2}，x=t$，围成图形（如图阴影部分）的面积为S，则函数S=g（t）的图象大致是（ ）
